Article contents
The determination of thermal stresses in dissimilar media
Published online by Cambridge University Press: 24 October 2008
Abstract
It is shown that if, in an infinite homogeneous unbounded elastic heat-conducting solid, we are given the thermal stresses 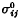 which arise when any arbitrarily shaped subregion of the upper half-space z > 0 is emitting any quantity of heat into the surrounding, then on introducing a different heat-conducting material into the half-space z < 0, the new thermal stresses
which arise when any arbitrarily shaped subregion of the upper half-space z > 0 is emitting any quantity of heat into the surrounding, then on introducing a different heat-conducting material into the half-space z < 0, the new thermal stresses 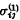 in z >0 and
in z >0 and 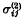 in z < 0 are explicitly expressible in an invariant form in terms of the known thermal stresses
in z < 0 are explicitly expressible in an invariant form in terms of the known thermal stresses 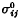 in the homogeneous infinite solid. Specialization of the derived dependence shows that the physically interesting interfacial discontinuities inherent in the problem admit the representation
in the homogeneous infinite solid. Specialization of the derived dependence shows that the physically interesting interfacial discontinuities inherent in the problem admit the representation
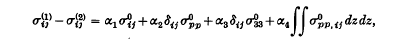
while the traction transmitted across the interface takes the form
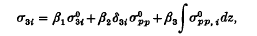
where αi and βi are constants. An application is then made to the case when the region emitting heat into the surrounding is ellipsoidal, since this is a fundamental shape of practical importance. Applications can however be made to any shape of the region emitting heat, provided that the corresponding harmonic and biharmonic potentials are available.
The paper may be considered to have its origin in the half-space theorem of Lorentz in hydrodynamics.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 3 , May 1981 , pp. 533 - 542
- Copyright
- Copyright © Cambridge Philosophical Society 1981
References
REFERENCES
- 3
- Cited by


