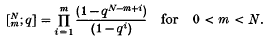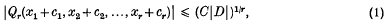Research Article
Some best-approximation theorems in tensor-product spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 385-390
-
- Article
- Export citation
How to solve a quadratic equation in integers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-5
-
- Article
- Export citation
A Lagrangian Klein bottle
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-200
-
- Article
- Export citation
Rigid homogeneous chains
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 07-17
-
- Article
- Export citation
A simple proof of the Mazur-Orlicz summability theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 391-392
-
- Article
- Export citation
Invariants of pencils of binary cubics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-209
-
- Article
- Export citation
The Torres conditions are insufficient
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-22
-
- Article
- Export citation
A note on a theorem of Maddox on strong almost convergence
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-396
-
- Article
- Export citation
Some identities for terminating q-series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 211-223
-
- Article
- Export citation
The inhomogeneous minimum of quadratic forms of signature ± 1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 225-235
-
- Article
- Export citation
On Morita's p-adic gamma function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-27
-
- Article
- Export citation
On the convergence of certain singular integrals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 397-403
-
- Article
- Export citation
Representation of an integer as a prime plus a product of two small factors
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 29-33
-
- Article
- Export citation
A characterization of two-dimensional unmixed local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 237-239
-
- Article
- Export citation
Noncommutative Lp-spaces with 0 < p < 1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 405-411
-
- Article
- Export citation
A pencil of four-nodal plane sextics
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 413-421
-
- Article
- Export citation
Bol loops of order pq
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 241-256
-
- Article
- Export citation
An extension of the Freiheitssatz
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 35-41
-
- Article
- Export citation
The structure of modules over polycyclic groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-283
-
- Article
- Export citation
On singularities, envelopes and elementary differential geometry
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-48
-
- Article
- Export citation

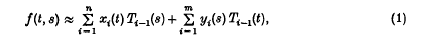
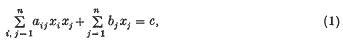
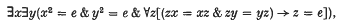
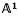 over
over 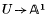
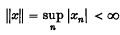 . A linear functional
. A linear functional 
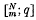 is the Gaussian polynomial denned to be zero for
is the Gaussian polynomial denned to be zero for