Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2025-01-01T16:35:27.480Z Has data issue: false hasContentIssue false
  • English
  • Français

Rigid homogeneous chains

Published online by Cambridge University Press:  24 October 2008

A. M. W. Glass ,
Yuri Gurevich ,
W. Charles Holland  and
Saharon Shelah
A. M. W. Glass
Affiliation:
Bowling Green State University, Bowling Green, Ohio 43403U.S.A.
Yuri Gurevich
Affiliation:
Ben-Gurion University of the Negev, Beer-Sheva, Israel.
W. Charles Holland
Affiliation:
Bowling Green State University, Bowling Green, Ohio 43403U.S.A.
Saharon Shelah
Affiliation:
The Hebrew University, Jerusalem, Israel
Get access Rights & Permissions [Opens in a new window]

Extract

Classifying (unordered) sets by the elementary (first order) properties of their automorphism groups was undertaken in (7), (9) and (11). For example, if Ω is a set whose automorphism group, S(Ω), satisfies

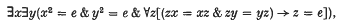
then Ω has cardinality at most ℵ0 and conversely (see (7)). We are interested in classifying homogeneous totally ordered sets (homogeneous chains, for short) by the elementary properties of their automorphism groups. (Note that we use ‘homogeneous’ here to mean that the automorphism group is transitive.) This study was begun in (4) and (5). For any set Ω, S(Ω) is primitive (i.e. has no congruences). However, the automorphism group of a homogeneous chain need not be o-primitive (i.e. it may have convex congruences). Fortunately, ‘o-primitive’ is a property that can be captured by a first order sentence for automorphisms of homogeneous chains. Hence our general problem falls naturally into two parts. The first is to classify (first order) the homogeneous chains whose automorphism groups are o-primitive; the second is to determine how the o-primitive components are related for arbitrary homogeneous chains whose automorphism groups are elementarily equivalent.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 89 , Issue 1 , January 1981 , pp. 07 - 17
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Baumgartner, J. E.All ℵ1-dense sets of reals can be isomorphic. Fund. Math. 79 (1973), 101–106.CrossRefGoogle Scholar
(2)Dushnik, B. and Miller, E. W.Concerning similarity transformations of linearly ordered sets. Bull. Amer. Math. Soc. 46 (1940), 322–326.CrossRefGoogle Scholar
(3)Glass, A. M. W.Ordered Permutation Groups, Bowling Green State University, Bowling Green, Ohio, 1976.1Google Scholar
(4)Gurevich, Y. and Holland, W. Charles.Recognizing the real line. Trans. Amer. Math. Soc. (To appear).Google Scholar
(5)Jambu-Giraudet, M. Théorie des modèles de groupes d'automorphisms d'ensembles totalement ordonnés, Thèse 3ème cycle, Université Paris VII, 1979.Google Scholar
(6)Jech, T. J.Lectures in Set Theory with Particular Emphasis on the Method of Forcing. Springer Lecture Notes 217, 1971.CrossRefGoogle Scholar
(7)Mckenzie, R.On elementary types of symmetric groups. Algebra Universalis, 1 (1971), 13–20.CrossRefGoogle Scholar
(8)Ohkuma, T.Sur quelques ensembles ordonnés linéairement. Fund. Math. 43 (1955), 326–337.Google Scholar
(9)Pinus, A. G.On elementary definability of symmetric groups and lattices of equivalences. Algebra Universalis, 3 (1973), 59–66.CrossRefGoogle Scholar
(10)Robinson, A. and Zakon, E.Elementary properties of ordered abelian groups. Trans. Amer. Math. Soc. 96 (1960), 222–236.CrossRefGoogle Scholar
(11)Shelah, S.First order theory of permutation groups. Israel J. Math. 14 (1973), 149–162; 15 (1973), 437–441.CrossRefGoogle Scholar
(12)Szmielew, W.Elementary properties of abelian groups. Fund. Math. 41 (1955), 203–271.CrossRefGoogle Scholar