Research Article
How to solve a quadratic equation in integers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-5
-
- Article
- Export citation
Rigid homogeneous chains
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 07-17
-
- Article
- Export citation
The Torres conditions are insufficient
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-22
-
- Article
- Export citation
On Morita's p-adic gamma function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 23-27
-
- Article
- Export citation
Representation of an integer as a prime plus a product of two small factors
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 29-33
-
- Article
- Export citation
An extension of the Freiheitssatz
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 35-41
-
- Article
- Export citation
On singularities, envelopes and elementary differential geometry
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-48
-
- Article
- Export citation
A constructive approach to the duality theorem for certain Orlicz spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-69
-
- Article
- Export citation
Sequences characterizing the sine function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 71-77
-
- Article
- Export citation
On maximal Euclidean sets avoiding certain distance configurations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-88
-
- Article
- Export citation
A quadratic mapping with invariant cubic curve
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 89-105
-
- Article
- Export citation
Rotation sets are closed
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-111
-
- Article
- Export citation
Homology of groups of surfaces in the 4-sphere
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-117
-
- Article
- Export citation
Orthomorphisms of archimedean vector lattices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-128
-
- Article
- Export citation
Lomonosov's hyperinvariant subspace theorem for real spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-133
-
- Article
- Export citation
Some inequalities for martingales and applications to the study of L1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-148
-
- Article
- Export citation
Existence of solutions of Hammerstein equations of compact type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 149-158
-
- Article
- Export citation
Shearing transformation of a linear system at an irregular singular point
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-166
-
- Article
- Export citation
Kneading of Lorenz type for intervals and product spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-179
-
- Article
- Export citation
On the Green's function for heterogeneous media in one-speed transport theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 181-192
-
- Article
- Export citation

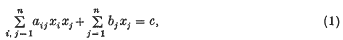
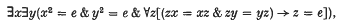
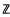

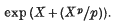

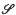 points in a Euclidean space has property
points in a Euclidean space has property 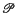 (2) if no 2 points
(2) if no 2 points 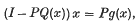

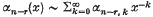 as
as 
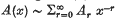 as
as 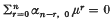 with multiplicity
with multiplicity 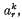 1 ≤
1 ≤