Research Article
The effect of twisting on the 2-Selmer group
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 513-526
-
- Article
-
- You have access
- Export citation
Ubiquity and large intersections properties under digit frequencies constraints
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 527-548
-
- Article
- Export citation
An algebraic generalization of Kripke structures†
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 549-577
-
- Article
- Export citation
Bases for commutative semigroups and groups
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 579-586
-
- Article
- Export citation
A criterion for a monomial in P(3) to be hit
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 587-599
-
- Article
- Export citation
A Cohen–Macaulay algebra has only finitely many semidualizing modules
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 601-603
-
- Article
- Export citation
Analytic continuation of multiple Hurwitz zeta functions
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 605-617
-
- Article
- Export citation
The threefold containing the Bordiga surface of degree ten as a hyperplane section
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 619-622
-
- Article
- Export citation
Hilbert polynomials and powers of ideals
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 623-642
-
- Article
- Export citation
The behaviour of solutions of the Gaussian curvature equation near an isolated boundary point
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 643-667
-
- Article
- Export citation
Exceptional sets for self-affine fractals
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 669-684
-
- Article
- Export citation
Invariant measures for meromorphic Misiurewicz maps
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 685-697
-
- Article
- Export citation
Complex asymptotics of Poincaré functions and properties of Julia sets
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 699-718
-
- Article
- Export citation
Hausdorff dimension of hairs and ends for entire maps of finite order
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 719-737
-
- Article
- Export citation
A devil's staircase from rotations and irrationality measures for Liouville numbers
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 739-756
-
- Article
- Export citation
Proceedings of Meetings
Proceedings of the meetings held during the session 2007–2008
-
- Published online by Cambridge University Press:
- 01 November 2008, pp. 757-763
-
- Article
- Export citation



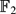
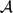
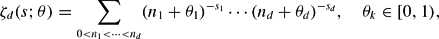
 , to locate the hyperplanes containing its possible poles and to compute the residues at the poles. We explain how to use the residues to locate trivial zeros of
, to locate the hyperplanes containing its possible poles and to compute the residues at the poles. We explain how to use the residues to locate trivial zeros of 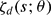 .
.
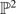 with
with 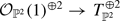 , where
, where 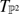 is the tangent bundle of
is the tangent bundle of 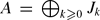 and
and  are finitely generated, we show the function
are finitely generated, we show the function 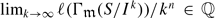 , if
, if