Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maeda, Hidetoshi
2008.
Threefolds containing Bordiga surfaces as ample divisors.
Proceedings of the American Mathematical Society,
Vol. 137,
Issue. 5,
p.
1631.


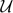 be a very ample vector bundle of rank 2 on
be a very ample vector bundle of rank 2 on 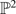 with
with 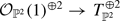 , where
, where 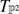 is the tangent bundle of
is the tangent bundle of 