Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T13:25:35.788Z Has data issue: false hasContentIssue false
  • English
  • Français

A criterion for a monomial in P(3) to be hit

Published online by Cambridge University Press:  01 November 2008

A. S. JANFADA
A. S. JANFADA*
Affiliation:
Department of Mathematics, Urmia University, P.O. Box 165, Urmia, Iran. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let P(n) = 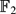[x1, . . ., xn] = ⊕d≥0Pd(n) be the polynomial algebra viewed as a graded left module over the Steenrod algebra 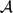at the prime 2. The grading is by the degree of the homogeneous polynomials Pd(n) of degree d in the n variables x1, . . ., xn. The algebra P(n) realizes the cohomology of the product of n copies of infinite real projective space. We recall that a homogeneous element f of grading d in a graded left 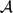-module M is hit if there is a finite sum f = ΣiSqi(hi), called a hit equation, where the pre-images hi ∈ M have grading strictly less than d and the Sqi, called the Steenrod squares, generate 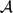. One of the important parts of the hit problem is to check whether a given polynomial in M is hit or not. In this article we study this problem in the 3-variable case.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 145 , Issue 3 , November 2008 , pp. 587 - 599
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Carlisle, D. P. and Wood, R. M. W.The Boundedness conjecture for the action of the Steenrod algebra on polynomials. Adams Memorial Symposium on Algebraic Topology, Vol. 2. London Math. Soc. Lecture Note Ser. 176 (Cambridge University Press, 1992), 203–216.Google Scholar
[2]Janfada, A. S. The hit problem for symmetric polynomials over the Steenrod algebra. Thesis. Manchester University (2000).Google Scholar
[3]Janfada, A. S. and Wood, R. M. W.The hit problem for symmetric polynomials over the Steenrod algebra. Math. Proc Camb. Phil. Soc. 133 (2002), 295–303.CrossRefGoogle Scholar
[4]Janfada, A. S. and Wood, R. M. W.Generating H*(BO(3), F_2) as a module over the Steenrod algebra. Math. Proc. Camb. Phil. Soc. 134 (2003), 239–258.CrossRefGoogle Scholar
[5]Kameko, M. Products of projective spacec as Steenrod modules. Thesis. John Hopkin University (1990).Google Scholar
[6]Kameko, M.Generators of the cohomology of BV3. J. Math. Kyoto Univ. 38 (1998), 587–593.Google Scholar
[7]Mosher, R. E. and Tangora, M. C.Cohomology Operations and Applications in Homology Theory Harper and Row (1968).Google Scholar
[8]Peterson, F. P.Generators of H*(RP∞ ∧ RP∞) as a module over the Steenrod algebra. Abstracts Amer. Math. Soc. (1987), 833–55–89.Google Scholar
[9]Silverman, J.Conjugation and excess in the Steenrod algebra. Proc. Amer. Math. Soc. 119 (1993), 657–661.CrossRefGoogle Scholar
[10]Singer, W.On the action of Steenrod squares on polynomial algebras. Proc. Amer. Math. Soc. 111 (1991), 577–583.CrossRefGoogle Scholar
[11]Steenrod, N. E. and Epstein, D. B. A.Cohomology operations. Ann. of Math. Stud. 50 (Princeton University Press, 1962).Google Scholar
[12]Wood, R. M. W.Steenrod squares of polynomials and the Peterson conjecture. Math. Proc. Camb. Phil. Soc. 105 (1989), 307–309.CrossRefGoogle Scholar
[13]Wood, R. M. W.Problems in the Steenrod algebra. Bull. London Math. Soc. 30 (1998), 449–517.CrossRefGoogle Scholar