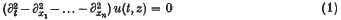Research Article
On the average order of the lattice rest of a convex planar domain
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-4
-
- Article
- Export citation
Refining the conditions on the Fermat quotient
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-8
-
- Article
- Export citation
Unbalanced quadratic residues and non-residues
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 9-17
-
- Article
- Export citation
Some examples of maximal orders
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 19-32
-
- Article
- Export citation
A note on asymptotically unmixed ideals
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-35
-
- Article
- Export citation
Transversal parameters and tangential flatness
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-49
-
- Article
- Export citation
On the bundle of principal connections and the stability of b-incompleteness of manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 51-59
-
- Article
- Export citation
Affine bundles and integrable almost tangent structures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 61-71
-
- Article
- Export citation
Note on uniform visibility manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 73-80
-
- Article
- Export citation
T1-locales
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 81-86
-
- Article
- Export citation
Equivariant self equivalences of principal fibre bundles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 87-92
-
- Article
- Export citation
Shake-slice knots and smooth contractible 4-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 93-106
-
- Article
- Export citation
Topological concordance and F-isotopy
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-110
-
- Article
- Export citation
Cancellation of hyperbolic ε-hermitian forms and of simple knots
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-115
-
- Article
- Export citation
An elementary proof of Gleason's theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-128
-
- Article
- Export citation
Ergodic measures are of weak product type
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-145
-
- Article
- Export citation
The Hausdorff dimension of limit sets of fuchsian groups of the type (g;m)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 147-154
-
- Article
- Export citation
Self-intersections of random walks on discrete groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 155-177
-
- Article
- Export citation
Note on propagation of classical waves: I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-181
-
- Article
- Export citation
An existence theorem for the discrete coagulation–fragmentation equations: II. Inclusion of source and efflux terms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 183-185
-
- Article
- Export citation

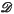 denote a compact convex subset of the Euclidean plane containing the origin as an inner point and assume that the boundary ∂
denote a compact convex subset of the Euclidean plane containing the origin as an inner point and assume that the boundary ∂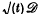 and define the ‘lattice rest’ by
and define the ‘lattice rest’ by 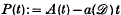 (where
(where 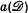 is the area of
is the area of 
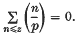
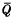 of
of 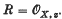 Let t = {
Let t = {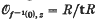 will be worse than that of
will be worse than that of 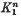 and
and 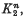 , we define their connected sum
, we define their connected sum 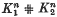 as in [13], p. 39. The cancellation problem for
as in [13], p. 39. The cancellation problem for