Transversal parameters and tangential flatness
Published online by Cambridge University Press: 24 October 2008
Extract
Let X be an algebraic variety over a field k, z a point of X and 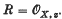 Let t = {t1..., ts} be part of a system of parameters of R. Then these parameters are algebraically independent over k, and therefore they define (near z) a projection f: X → As(k) to an s-dimensional affine space over k, sending z to the origin 0∊s(k). In general, the Hilbert function (resp. multiplicity) of
Let t = {t1..., ts} be part of a system of parameters of R. Then these parameters are algebraically independent over k, and therefore they define (near z) a projection f: X → As(k) to an s-dimensional affine space over k, sending z to the origin 0∊s(k). In general, the Hilbert function (resp. multiplicity) of 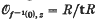 will be worse than that of
will be worse than that of 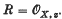 , and we will call the system t transversal, if the Hilbert function (resp. multiplicity) of R and R/tR agree. This gives two notions of transversality: one for Hilbert functions (H-transversal), and a weaker one for multiplicities (e-transversal). For s = dim R we recover the notion of a transversal system of parameters introduced by Zariski for studying equisingularity problems (see e.g. [17]). In the above set-up the numerical characters are defined with respect to the maximal ideal of R, but we will consider this problem for arbitrary ideals I using generalized Hilbert functions of type H[x, I, R] (see [7] and [10]).
, and we will call the system t transversal, if the Hilbert function (resp. multiplicity) of R and R/tR agree. This gives two notions of transversality: one for Hilbert functions (H-transversal), and a weaker one for multiplicities (e-transversal). For s = dim R we recover the notion of a transversal system of parameters introduced by Zariski for studying equisingularity problems (see e.g. [17]). In the above set-up the numerical characters are defined with respect to the maximal ideal of R, but we will consider this problem for arbitrary ideals I using generalized Hilbert functions of type H[x, I, R] (see [7] and [10]).
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 1 , July 1985 , pp. 37 - 49
- Copyright
- Copyright © Cambridge Philosophical Society 1985
References
REFERENCES
- 2
- Cited by


