If G is a group of finite order which contains an operation P of prime order p, permutable only with its own powers, the order of G must, by Sylow's theorem, be of the form (1 + kp) pś, where s is a factor of p – 1. The greatest subgroup of G, which contains self-conjugately {P};, the subgroup generated by P, must be a metacyclical subgroup {S, P}, where
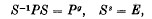
while g is a primitive root of the congruence gs = 1 (mod. p).