No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 24 October 2008
If G is a group of finite order which contains an operation P of prime order p, permutable only with its own powers, the order of G must, by Sylow's theorem, be of the form (1 + kp) pś, where s is a factor of p – 1. The greatest subgroup of G, which contains self-conjugately {P};, the subgroup generated by P, must be a metacyclical subgroup {S, P}, where
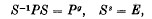
while g is a primitive root of the congruence gs = 1 (mod. p).
* Burnside, , Theory of Groups, § 221.Google Scholar
† Loc. cit. § 221.
‡ Loc., cit. § 234.
§ Loc. cit. § 218.
* Loc. cit. §§ 234, 235.
† Loc. cit. § 218.
* Loc. cit. § 219.
* Loc. cit. § 243.