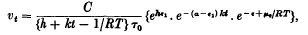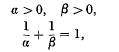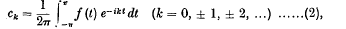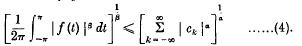Research Article
A Generalization of Feuerbach's Theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 601-620
-
- Article
- Export citation
Characteristics of complexes of conics in space of four dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 621-629
-
- Article
- Export citation
Note on the Lorentz group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 630-632
-
- Article
- Export citation
The Symmetric Functions of which the General Determinant is a particular case
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 633-654
-
- Article
- Export citation
On simplexes doubly incident with a quadric
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 655-668
-
- Article
- Export citation
On the phrase “equally probable.”
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 669-671
-
- Article
- Export citation
A note on wireless signal strength measurements made during the Solar Eclipse of 24 January, 1925
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 672-675
-
- Article
- Export citation
The Action of the Electrical Counter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 676-683
-
- Article
- Export citation
An extension of Wallace's, Miguel's and Clifford's theorems on circles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 684-687
-
- Article
- Export citation
Triple Binary Forms; the complete system for a single (1, 1, 1) form with its geometrical interpretation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 688-693
-
- Article
- Export citation
A Geometrical treatment of the Correspondence between Lines in Threefold Space and Points of a Quadric in Fivefold space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 694-699
-
- Article
- Export citation
Theory of Statistical Estimation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 700-725
-
- Article
- Export citation
On the idea of frequency
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 726-727
-
- Article
- Export citation
The bursting of soap-bubbles in a uniform electric field
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 728-730
-
- Article
- Export citation
The passage of electrons through small apertures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 731-737
-
- Article
- Export citation
An apparatus for the investigation of the effect of poisonous substances, and mixed vapours on catalytic activity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 738-750
-
- Article
- Export citation
On Pedal Quadrics in Non-Euclidean Hyperspace
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 751-758
-
- Article
- Export citation
The temperature distribution in a transformer or other laminated core of rectangular cross section in which heat is generated at a uniform rate
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 759-772
-
- Article
- Export citation
The theory of the influence of magnetic fields on the stopping power of gases for α-particles
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 773-776
-
- Article
- Export citation
On Hausdorff's proof of the extended Riesz-Fischer theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 777-778
-
- Article
- Export citation

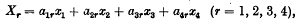
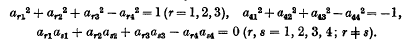
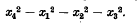
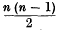 lines
lines 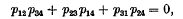
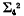 of four dimensions in five dimensional space,
of four dimensions in five dimensional space, 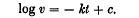
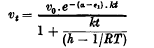
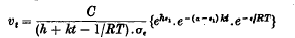
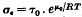 , where τ
, where τ