Research Article
A generalization of the Königsberg bridges problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-4
-
- Article
- Export citation
The non-existence of a certain finite projective plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-12
-
- Article
- Export citation
On the crystallography of infinite Coxeter groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 13-24
-
- Article
- Export citation
The associated graded ring of an integral group ring
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-33
-
- Article
- Export citation
Some unexpectedly non-singular orbit spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 35-37
-
- Article
- Export citation
Injective W*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 39-47
-
- Article
- Export citation
Spectra of derivations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-57
-
- Article
- Export citation
On separation axioms for certain types of ordered topological space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 59-65
-
- Article
- Export citation
Closed graph theorems for generalized inductive limit topologies
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-83
-
- Article
- Export citation
Weakly compactly generated locally convex spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 85-98
-
- Article
- Export citation
On 2-dimensional homology classes of 4-manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-106
-
- Article
- Export citation
Consistency and Nörlund means
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-109
-
- Article
- Export citation
The evaluation in terms of Γ-functions of the periods of elliptic curves admitting complex multiplication
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-118
-
- Article
- Export citation
Some generalizations of the Borsuk–Ulam theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 119-125
-
- Article
- Export citation
The uniqueness of Atkinson and Reuter's epidemic waves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-130
-
- Article
- Export citation
Bounds for the solution of a non-linear parabolic initial-boundary value problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-145
-
- Article
- Export citation
On Legendre transformations and elementary catastrophes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 147-163
-
- Article
- Export citation
On the crystallographic point groups and on Cauchy symmetry
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-175
-
- Article
- Export citation
Front matter
PSP volume 82 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 82 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

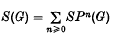 the symmetric algebra of
the symmetric algebra of 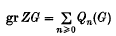 the associated graded ring of the integral group ring
the associated graded ring of the integral group ring 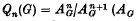 (
(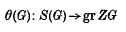
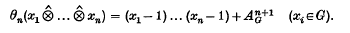
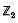 given by the matrix.
given by the matrix.
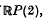
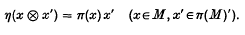
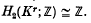 ).
).
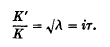
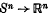 are continuous and the degree of
are continuous and the degree of