Research Article
A note on inequivalence of realizability toposes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-3
-
- Article
- Export citation
Zeros and poles of Artin L-series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 5-11
-
- Article
- Export citation
Special values of L-functions and height two formal groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 13-24
-
- Article
- Export citation
On a certain class of group presentations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-35
-
- Article
- Export citation
Unipotent normal subgroups of skew linear groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-51
-
- Article
- Export citation
Ringing the cosets. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 53-65
-
- Article
- Export citation
Representation of tiled matrix rings as full matrix rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-72
-
- Article
- Export citation
Certain countably generated big Cohen-Macaulay modules are balanced
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 73-77
-
- Article
- Export citation
Families of Jacobian manifolds and characteristic classes of surface bundles. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-101
-
- Article
- Export citation
Some link-polynomial relations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-107
-
- Article
- Export citation
Nets of quadrics and deformations of Σ3〈3〉 singularities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-115
-
- Article
- Export citation
Lifting results for sequences in Banach spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-121
-
- Article
- Export citation
The spectrum of the Cesàro operator on c0(c0)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-129
-
- Article
- Export citation
A note on real H*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-132
-
- Article
- Export citation
Isometries of self-adjoint complex function spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 133-138
-
- Article
- Export citation
Yet another short proof of the Riesz representation theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-140
-
- Article
- Export citation
A nonstandard proof of the Riesz representation theorem for weakly compact operators on C(Ω)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 141-145
-
- Article
- Export citation
Power-bounded elements and tauberian theorems in locally convex algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 147-159
-
- Article
- Export citation
Spectral decay for definite kernels and functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-163
-
- Article
- Export citation
Singular numbers of smooth kernels. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 165-167
-
- Article
- Export citation

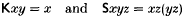
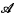 for the realizability topos constructed from
for the realizability topos constructed from  of discriminant −
of discriminant −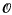 of
of 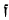 and fix a Weierstrass model for
and fix a Weierstrass model for 
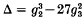 is divisible only by primes dividing 6
is divisible only by primes dividing 6
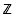 ). In this paper we deal with the case of Σ
). In this paper we deal with the case of Σ
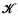 equivalence. The classification of such nets involves a single parameter
equivalence. The classification of such nets involves a single parameter 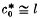 and showing that the operator (
and showing that the operator (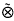
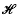
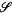 (
(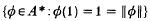
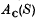 , and re
, and re 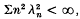 is, of course, stronger than λ
is, of course, stronger than λ