Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T01:25:57.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Nets of quadrics and deformations of Σ3〈3〉 singularities

Published online by Cambridge University Press:  24 October 2008

S. A. Edwards  and
C. T. C. Wall
S. A. Edwards
Affiliation:
Department of Pure Mathematics, University of Liverpool
C. T. C. Wall
Affiliation:
Department of Pure Mathematics, University of Liverpool
Get access Rights & Permissions [Opens in a new window]

Extract

The 2-jet of a Σ3 map-germ f:(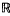3, 0) → (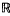3, 0) determines a net of quadratic maps from 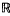3 to 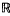3; for nets of general type this jet is sufficient for 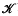equivalence. The classification of such nets involves a single parameter c. It is shown in [7], also in [3], that the versai unfolding of f is topologically trivial over the parameter space. However, there are 4 connected components of this space of nets. The main object of this paper is to show that the corresponding unfolded maps are of different topological types.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 1 , January 1989 , pp. 109 - 115
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Damon, J. N. and Galligo, A.. A topological invariant for stable map-germs. Invent. Math. 32 (1976), 103–132.Google Scholar
[2]Damon, J. N.. Topological properties of discrete algebra types II: real and complex algebras. Amer. J. Math. 101 (1979), 1219–1248.Google Scholar
[3]Damon, J. N.. Finite determinacy and topological triviality II: sufficient conditions and topological stability. Compositio Math. 47 (1982), 101–132.Google Scholar
[4]Edwards, S. A.. On the local topological classification of real stable map-germs. Ph.D. thesis, Liverpool University (1987).Google Scholar
[5]Edwards, S. A. and Wall, C. T. C.. The stable topological type of finite map-germs. (To appear.)Google Scholar
[6]Hellebrand, S.. Deformation dicker Punkte und Netze von Quadriken. Regensburger Math. Schriften 9 (1985).Google Scholar
[7]Ronga, F., Une application topologiquement stable qui ne peut pas être approchée par une application différentiablement stable. C. R. Acad. Sci. Paris Sér. I Math. 287 (1978), 779–782.Google Scholar
[8]Wall, C. T. C.. Nets of conics. Math. Proc. Cambridge Philos. Soc. 81 (1977), 351–364.CrossRefGoogle Scholar
[9]Wall, C. T. C.. Nets of quadrics, and theta-characteristics of singular curves. Philos. Trans. Roy Soc. London Ser. A 289 (1978), 229–269.Google Scholar
[10]Wall, C. T. C.. Singularities of nets of quadrics. Compositio Math. 42 (1981), 187–212.Google Scholar