Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T01:20:37.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular numbers of smooth kernels. II

Published online by Cambridge University Press:  24 October 2008

Charles Oehring
Charles Oehring
Affiliation:
Virginia Polytechnic Institute and State University, Blacksburg, Virginia 24061, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

Reade[10] has recently improved Weyl's classical estimate λn = o(n−3/2) for the eigenvalues of a symmetric kernel K∈C1 by relaxing the Cl hypothesis to the assumptions that K∈L2[0, 2π]2, that K is absolutely continuous in each variable separately, and that both ∂K/∂s and ∂K/t belong to L2[0, 2π]2. The conclusion of his theorem, that 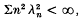is, of course, stronger than λn = o(n−3/2).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 105 , Issue 1 , January 1989 , pp. 165 - 167
Copyright
Copyright © Cambridge Philosophical Society 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cochran, J. A.. The nuclearity of operators generated by Hölder continuous kernels. Math. Proc. Cambridge Philos. Soc. 75 (1974), 351–356.CrossRefGoogle Scholar
[2]Cochran, J. A.. Summability of singular values of L 2 kernels-analogies with Fourier series. Enseign. Math. (2) 22 (1976), 141–157.Google Scholar
[3]DeLeeuw, K., Katznelson, Y. and Kahane, J.. Sur les coefficients de Fourier des fonctions continues. C. R. Acad. Sci. Paris, Sér. A 285 (1977), 1001–1003.Google Scholar
[4]Dunford, N. and Schwartz, J.. Linear Operators. Part II. Spectral Theory (Interscience, 1963).Google Scholar
[5]Halmos, P. and Sunder, V.. Bounded Integral Operators on L 2 Spaces (Springer-Verlag, 1978).CrossRefGoogle Scholar
[6]Knopp, K.. Theory and Application of Infinite Series (Blackie, 1951).Google Scholar
[7]Oehring, C.. Singular numbers of smooth kernels. Math. Proc. Cambridge Philos. Soc. 103 (1988), 511–514.CrossRefGoogle Scholar
[8]Oehring, C.. Asymptotics of singular numbers of smooth kernels via trigonometric transforms. J. Math. Anal. App. (To appear.)Google Scholar
[9]Gohberg, I. and Krein, M.. Introduction to the Theory of Linear Nonselfadjoint Operators (American Mathematical Society, 1969).Google Scholar
[10]Reade, J. B.. Eigenvalues of smooth kernels. Math. Proc. Cambridge Philos. Soc. 95 (1984), 135–140.CrossRefGoogle Scholar
[11]Reade, J. B.. On the sharpness of Weyl's estimate for eigenvalues of smooth kernels. SIAM J. Math. Anal. 16 (1985), 548–550.CrossRefGoogle Scholar
[12]Smithies, F.. Integral Equations (Cambridge University Press, 1962).Google Scholar
[13]Triebel, H.. Über die Verteilung der Approximationszahlen kompakter Operatoren in Sobolev-Besov Räumen. Invent. Math. 4 (1967), 275–293.CrossRefGoogle Scholar
[14]Zygmund, A.. Trigonometric Series, vol. 1 (Cambridge University Press, 1959).Google Scholar
[15]Zygmund, A.. Trigonometric Series, vol. 2 (Cambridge University Press, 1959).Google Scholar