Research Article
Non-Relativistic Dispersion Relations for a Two Channel Scattering Process
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 363-376
-
- Article
- Export citation
Transition Integrals for Si IV and CaII
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 377-381
-
- Article
- Export citation
Diffraction by a Screen Causing Large Random Phase Fluctuations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 382-400
-
- Article
- Export citation
The Effect of a Magnetic Pole on the Energy Levels of a Hydrogen-Like Atom
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 401-404
-
- Article
- Export citation
On Viscous Flow in a Pipe with Constrictions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 405-416
-
- Article
- Export citation
Bounds for the Torsional Rigidity of Isotropic Beams
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-419
-
- Article
- Export citation
Research Notes
Equally Inclined Spheres
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 420-421
-
- Article
- Export citation
A Note on the Vague Topology for Measures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-422
-
- Article
- Export citation
A Uniqueness Theorem for the Exponential Series of Herglotz (II)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 422-425
-
- Article
- Export citation
Some Cyclic and Other Inequalities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 425-427
-
- Article
- Export citation
Asymptotic Cumulants for Distributions of k-State Markov Chains
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 427-430
-
- Article
- Export citation
A Note on Characteristic Functions Which Vanish Identically in an Interval
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 430-432
-
- Article
- Export citation
Front matter
PSP volume 58 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 58 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation





 is the Fourier transform of the potential
is the Fourier transform of the potential 
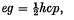
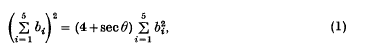
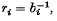 , where
, where 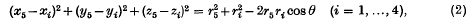
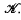 The Riesz-Markov theorem shows that there is a 1−1 correspondence between the set of regular Borel measures on
The Riesz-Markov theorem shows that there is a 1−1 correspondence between the set of regular Borel measures on 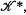 the topological dual of
the topological dual of 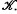 . Let {μ
. Let {μ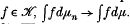 . Thus the vague topology is that of simple convergence in
. Thus the vague topology is that of simple convergence in 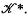 . We shall call a μ-measurable set μ-quarrable if its boundary is a μ-null set.
. We shall call a μ-measurable set μ-quarrable if its boundary is a μ-null set.