A Note on the Vague Topology for Measures

Extract

We refer for general background to N. Bourbaki, Intégration, chapters iv and v. We consider a locally compact Hausdorff space R and denote the set of continuous functions with compact support by 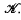The Riesz-Markov theorem shows that there is a 1−1 correspondence between the set of regular Borel measures on R and the set of positive elements of 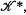the topological dual of 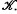. Let {μ_n}, μ be regular Borel probability measures on R. The sequence of measures {μ_n} is said to converge vaguely to μ if, for all 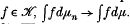. Thus the vague topology is that of simple convergence in 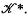. We shall call a μ-measurable set μ-quarrable if its boundary is a μ-null set.