Introduction. Hall ((3), (4)) introduced the concept of a Sylow system and its normalizer into the theory of finite soluble groups. In (4) he showed that system normalizers may be characterized as those subgroups D of G minimal subject to the existence of a chain of subgroups from D up to G in which each subgroup is maximal and non-normal in the next; he also showed that a system normalizer covers all the central chief factors and avoids all the eccentric chief factors of G (for definitions of covering and avoidance, and an account of their elementary properties), the reader is referred to Taunt ((5)). This note arises out of an investigation into the question to what extent this covering/ avoidance property characterizes system normalizers; it provides a partial answer by means of two elementary counter-examples given in section 3 which seem to indicate that the property ceases to characterize system normalizers as soon as the ‘non-commutativity’ of the group is increased beyond a certain threshold. For the sake of completeness we include proofs in Theorems 1 and 2 of generalizations of two known results communicated to me by Dr Taunt and which as far as we know have not been published elsewhere. Theorem 1 shows the covering/avoidance property to be characteristic for the class of soluble groups with self-normalizing system normalizers introduced by Carter in (1), while Theorem 2 shows the same is true for A -groups (soluble groups with Abelian Sylow subgroups investigated by Taunt in (5)).

Introduction. In this note we obtain a description of the structure of the minimal verbal subgroups of a finite group which has, among others, the following consequences:

Theorem 1. A finite group which belongs to the variety generated by its proper subgroups and proper factor-groups belongs either to the variety generated by its proper subgroups or to the variety generated by its proper factor-groups.

Introductory. In the following pages a miscellany of information about M12, the Mathieu group of degree 12, is presented, mainly concerning its subgroups. The development is inspired by the work of Coxeter and Todd on the representation of M12 as a group of collineations in PG (5,3)—i.e. five-dimensional projective space over the field of 3 elements.

Introduction. In (1–3,6) it is shown that homological algebra can be applied to stable homotopy-theory. In this application, we deal with A -modules, where A is the mod p Steenrod algebra. To obtain a concrete geometrical result by this method usually involves work of two distinct sorts. To illustrate this, we consider the spectral sequence of (1,2):

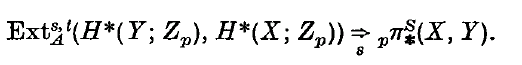
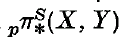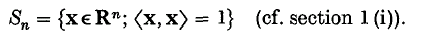
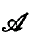Here each group Extss, t which occurs in the E2 term can be effectively computed; the process is purely algebraic. However, no such effective method is given for computing the differentials dr in the spectral sequence, or for determining the group extensions by which is built up from the E∞ term; these are topological problems.

Summary of results. In this paper we shall study some properties of the algebra A(Rn) for n ≥ 1 relative to the unit sphere

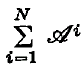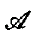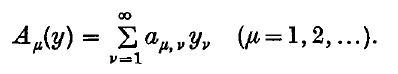
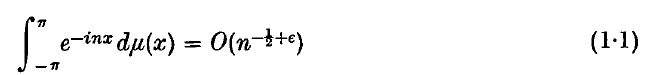
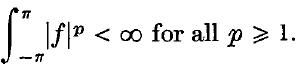Let A = (am, n) be a (regular summability) matrix. Then will denote the set of bounded sequences which are summed by A. If {Ai} (i = 1, 2, …, N) is a finite set of such matrices, and if consists of every bounded sequence then we shall say that the matrices span the bounded sequences. Ifx = {xn} belongs to then we denote the value to which A sums x by A-lim x. If y = {yn} is any sequence, then the A-transform of y (if it exists) is the sequence {Aμ(y)}, where

Introduction. It is a classical problem to construct a complex projective space, using as ‘imaginary points’ objects of some kind from the geometry of real projective space. (The various solutions to this problem have been reviewed in a book by Coolidge ((1)).) The object of the present paper is to solve the corresponding problem for n-dimensional projective spaces over two skew fields, one being a second-rank extension of the other. The method used seems not to have been published before, even in connexion with the classical problem.

Introduction. A famous construction of Wiener and Wintner ((13)), later refined by Salem ((11)) and extended by Schaeffer ((12)) and Ivašev-Musatov ((8)), produces a non-negative, singular, continuous measure μ on [ − π,π[ such that

for every ∈ > 0. It is plain that the convolution μ * μ is absolutely continuous and in fact has Lebesgue–Radon–Nikodým derivative f such that For general locally compact Abelian groups, no exact analogue of (1 · 1) seems possible, as the character group may admit no natural order. However, it makes good sense to ask if μ* μ is absolutely continuous and has 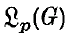pth power integrable derivative. 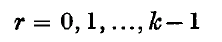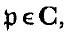We will construct continuous singular measures μ on all non-discrete locally compact Abelian groups G such that μ * μ is a absolutely continuous and for which the Lebesgue–Radon–Nikodým derivative of μ * μ is in, for all real p > 1.

Statement of results. Let A and B be two matrix summability methods, and S a given set of sequences. We shall say that B is S-stronger than A if B sums every sequence which belongs to S and is summed by A. If each of A, B is S-stronger than the other, A and B will be called S-equivalent. If B is S-stronger than A, but A is not S-stronger than B, we say that B is strictly S-stronger than A.

Let p be a prime and let f(x) be a quartic polynomial with integral coefficients. I consider the problem of estimating the least non-negative non-residue k of f(x) (modp) (I omit the mod p hereafter), for large primes p, so f(x) ≡ r has a solution for

but not for r = k. The same problem for cubics has been considered by Mordell ((1)), who showed that

as p → ∞, where the constant implied in the O-symbol is independent of the coefficients of the cubic. In fact a more detailed examination of Mordell's proof gives the better estimate

It is the purpose of this paper to show that this same estimate also holds for quartic polynomials.

We use the notations and definitions of the introduction to the previous paper ((1)), and say that 2 lattices K and L on a quadratic space over R(t) with its Dedekind set C are in the same genus if, for all , the lattices 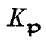and 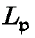are in the same class. We mean to count the number of classes of lattices in a given genus over a binary space: we shall find that it is either 1 or .

Introduction. In this paper, a study is made of the solutions of Lamé's differential equation as series of associated Legendre functions. The particular feature studied is the representation of the second solution corresponding to the case when the first solution is a Lamé polynomial.

The integral, involving the functions Jn+½ and J−n−½(x) where n is a positive integer, arises in a problem in electrical network theory and represents a measure of the overall error in the diagonal Padé approximant to the function e−s. A method of evaluation based on Euler's transformation of series is described, values of the integral are tabulated to five decimal places for n = 1(1)10(5)40, and the asymptotic behaviour for large n is determined.

Introduction. The object of this paper is to prove some formulae for Jacobi polynomials. The formulae (6), (7), (9), (10) and (13) are believed to be new.

The Feynman integral is evaluated for classical waves using a Hamiltonian approach to the summation over histories.

Recently Fox ((5)) has given an inversion formula for the transform whose kernel is xνKν(x), where Kν(x) is the modified Bessel function of the second kind, by the application of fractional integration theory. In the present paper it has been shown that the integral equation

can be thrown into the form of a Laplace integral, with the help of fractional integration, which can be solved by known methods.

Introduction. Agarwalin 1953 ((1)) gave the most general transformations involving bilateral cognate trigonometrical series of the hypergeometric type. Later, Shukla in 1957 ((2)) gave certain relations involving the products of two bilateral hypergeometric series. In this paper an attempt has been made to establish certain new transformations involving the products of two and more bilateral hypergeometric type of series. (For notations and definitions see Agarwal ((1)).)

By representing integral operators defined by kernels involving Bessel functions as compositions of two operators, we determine their mapping properties and, in one case, derive an inversion process. The operators considered are of the form

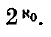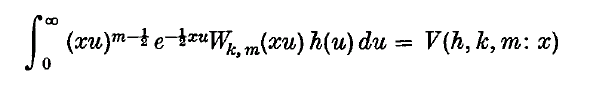
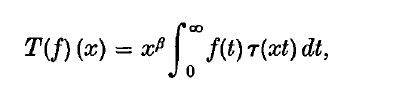
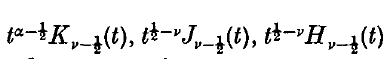where τ(t) is given respectively by and 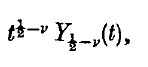and in the last three cases the integrals converge in norm.

Introduction. The subject of the mixtures of probability distributions has aroused a fresh interest in the fields of probability and statistics. Several authors, including Blischke, Rider, Robbins, Teicher, Patil and Seshadri, have discussed a variety of the associated probabilistic and statistical problems in varying details in the recent past. This paper attempts to solve by using the methods of infinite matrices some of the problems of the identifiability of countable mixtures of discrete probability distributions. It appears that here is still another area where Mathematics and Statistics can help one another grow. We are extremely thankful to Dr P. Vermes of Birkbeck College of the University of London for developing some theory of infinite matrices relevant to a couple of problems discussed in this paper. While most of the results discussed below are believed to be new, a few of them can be shown to be immediate consequences of a powerful result due to Teicher ((7)) obtained by using a different approach.

We describe some properties of a stationary, isolated, axially symmetric, rotating body of perfect fluid, according to general relativity. We first specialize to the case of constant specific entropy and constant angular velocity. The latter condition is equivalent to rigidity in the Born sense; both conditions are consequences of a simple variational principle. The hydrodynamic equations can then be integrated completely. Analogous first integrals are given also for the case of differential rotation. No use is made of the full field equations.