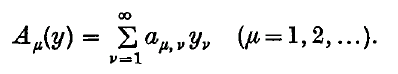Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Baker, J. W.
and
Petersen, G. M.
1967.
Summability fields which span the bounded sequences.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 63,
Issue. 1,
p.
99.
Petersen, Gordon M.
1974.
Linear Operators and Approximation II / Lineare Operatoren und Approximation II.
Vol. 25,
Issue. ,
p.
533.
Kangro, G. F.
1976.
Theory of summability of sequences and series.
Journal of Soviet Mathematics,
Vol. 5,
Issue. 1,
p.
1.


 will denote the set of bounded sequences which are summed by
will denote the set of bounded sequences which are summed by 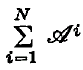 consists of every bounded sequence then we shall say that the matrices
consists of every bounded sequence then we shall say that the matrices 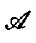 then we denote the value to which
then we denote the value to which