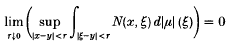Research Article
Examples of 3-knots with no minimal Seifert manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 417-420
-
- Article
- Export citation
Cofiniteness and vanishing of local cohomology modules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-429
-
- Article
- Export citation
Products of idempotent integer matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 431-441
-
- Article
- Export citation
Hall–Littlewood polynomials at roots of 1 and modular representations of the symmetric group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 443-453
-
- Article
- Export citation
Continuity of derivations on Mal'cev H*-algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 455-459
-
- Article
- Export citation
On complete curves in moduli space I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 461-466
-
- Article
- Export citation
On complete curves in moduli space II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 467-472
-
- Article
- Export citation
Twisting formulae of the Jones polynomial
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 473-482
-
- Article
- Export citation
Tauberian theorems for general power series methods
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 483-490
-
- Article
- Export citation
A cohomological characterization of amenable actions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 491-504
-
- Article
- Export citation
Strictly singular and strictly cosingular operators on spaces of continuous functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 505-521
-
- Article
- Export citation
Unremovable periodic orbits of homeomorphisms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 523-531
-
- Article
- Export citation
Polynomial expansions of positive harmonic functions in the unit ball
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 533-544
-
- Article
- Export citation
Near-constancy phenomena in branching processes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 545-558
-
- Article
- Export citation
Spectral characterization of the Wold–Zasuhin decomposition and prediction-error operator
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 559-567
-
- Article
- Export citation
Word problems related to derivatives of the displacement map
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 569-579
-
- Article
- Export citation
Continuity of solutions of Schrödinger equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 581-597
-
- Article
- Export citation
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 599
-
- Article
-
- You have access
- Export citation
Proceedings at the meetings
Proceedings at the meetings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 601-607
-
- Article
- Export citation
Front matter
PSP volume 110 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation

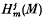 are known to be Artinian. Grothendieck [3], exposé 13, 1·2 made the following conjecture:
are known to be Artinian. Grothendieck [3], exposé 13, 1·2 made the following conjecture: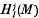 ) is finitely generated.
) is finitely generated.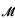
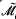
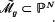 with hypersurfaces in sufficiently general position one obtains a complete curve in
with hypersurfaces in sufficiently general position one obtains a complete curve in 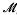
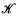 be an oriented knot in
be an oriented knot in 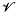 a solid torus endowed with a preferred framing which contains
a solid torus endowed with a preferred framing which contains 
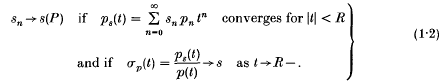
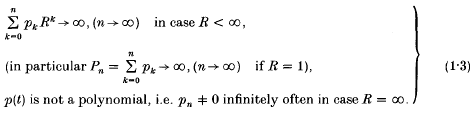
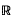
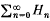 converges absolutely and locally uniformly to
converges absolutely and locally uniformly to 
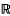 (where
(where