Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T14:03:32.842Z Has data issue: false hasContentIssue false
  • English
  • Français

Tauberian theorems for general power series methods

Published online by Cambridge University Press:  24 October 2008

R. Kiesel  and
U. Stadtmüller
R. Kiesel
Affiliation:
University of Ulm, Germany
U. Stadtmüller
Affiliation:
University of Ulm, Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Let us assume throughout that (pn) denotes a sequence of reals which satisfies

For real sequences (sn) with increments an = sn – sn−1 for n ≥ 0,(where s−1 = 0), we consider the power seriesmethod of summability (P), where we say

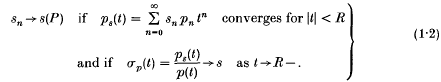
The power series methods (P) containthe so-called (Jp)-methods (R = 1)and the Borel-type methods (Bp)(R = ∞). We consider only regular (P)-methods, i.e. sn → s implies sn → s(P). By theorem 5 in [5], p.49, we have regularity if and only if

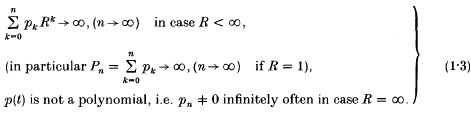
Here we are interested in the converse conclusion, namely sn → s(P) implies sn → s, which can only be validiffurther conditions, so-called Tauberian conditions are satisfied by (sn). These so-called Tauberian theorems for power series methods have a long history; see e.g. the books [5, 14, 23], and they found new attentionrecently in the papers [6, 18, 19, 20] and [8, 9, 10, 11, 12]. The latter papers contain certain o- Tauberian theorems for all power series methods in question and O-Tauberian theorems, if the weight sequence (pn) can be interpolated by alogarithmico-exponential function g(·)(see e.g. [4]), i.e.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 3 , November 1991 , pp. 483 - 490
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bingham, N. H., Goldie, C. M. and Teugels, J. L.. Regular Variation (Cambridge University Press, 1987).CrossRefGoogle Scholar
[2]Borwein, D. and Kkatz, W.. On relations between weighted mean and power series methods of summability. J. Math. Anal. Appl. 139 (1989), 178–186.CrossRefGoogle Scholar
[3]Borwein, D. and Markovich, T.. A Tauberian theorem concerning Borel-type and Cesàro methods of summability. Canad. J. Math. 40 (1988), 228–247.CrossRefGoogle Scholar
[4]Hardy, G. H.. Properties of logarithmico-exponential functions. Proc. London Math. Soc. (2) 10 (1911), 54–90.Google Scholar
[5]Hardy, G. H.. Divergent Series (Oxford University Press, 1949).Google Scholar
[6]Jakimovski, A. and Tietz, H.. Regularly varying functions and power series methods. J. Math. Anal. Appl. 73 (1980), 65–84CrossRefGoogle Scholar
Errata Jakimovski, A. and Tietz, H.. Regularly varying functions and power series methods. J. Math. Anal. Appl. 95 (1983), 597–598.CrossRefGoogle Scholar
[7]Kales, M. L.. Tauberian theorems related to Borel and Abel summability. Duke Math. J. 3 (1937), 647–666.CrossRefGoogle Scholar
[8]Kiesel, R.. Taubersätze und starke Gesetze für Potenzreihenverfahren. Dissertation, Universität Ulm (1990).Google Scholar
[9]Kratz, W. and Stadtmüller, U.. Tauberian Theorems for (Jp)-Summability. J. Math. Anal. Appl. 139 (1989), 362–371.CrossRefGoogle Scholar
[10]Kratz, W. and Stadtmüller, U.. Tauberian Theorems for general (Jp)-methods and a characterization of dominated variation. J. London Math. Soc. (2) 39 (1989), 145–159.CrossRefGoogle Scholar
[11]Kratz, W. and Stadtmüller, U.. O-Tauberian Theorems for (Jp)-methods with rapidly increasing weights. J. London Math. Soc. (2) 41 (1990), 489–502.CrossRefGoogle Scholar
[12]Kratz, W. and Stadtmüller, U.. Tauberian Theorems for Borel-type methods of summability. Arch. Math. (Basel) 55 (1990), 465–474.CrossRefGoogle Scholar
[13]Kwee, B.. A Tauberian theorem for the (J, pn) method of summation. J. London Math. Soc. (2) 5 (1972), 139–142.CrossRefGoogle Scholar
[14]Peyerimhoff, A.. Lectures on Summability. Lecture Notes in Math. vol. 107 (Springer-Verlag, 1969).Google Scholar
[15]Rangachari, M. S.. Tauberian oscillation theorems for the summability methods of the Hardy family. Indian J. Math. 22 (1980), 225–243.Google Scholar
[16]Schmidt, R.. Die Umkehrsätze des Borel'schen Summierungsverfahrens. Schriften Königsberg 1 (1925), 205–265.Google Scholar
[17]Seneta, E.. Regularly Varying Functions. Lecture Notes in Math. vol. 508 (Springer-Verlag, 1976).CrossRefGoogle Scholar
[18]Tietz, H.. Schmidt'sche Umkehrbedingungen für Potenzreihenverfahren. Ada Sci. Math. (Szeged), to appear.Google Scholar
[19]Tietz, H.. Tauberian theorems of (Jv)→(Mp)-type. Math. J. Okayama Univ. 31 (1989), 221–225.Google Scholar
[20]Tietz, H.. and Trautner, R.. Tauber-Sätze für Potenzreihenverfahren. Arch. Math. (Basel) 50 (1988), 164–174.CrossRefGoogle Scholar
[21]Vijayaraghavan, T.. A Tauberian Theorem. J. London Math. Soc. (1) (1926), 113–120.CrossRefGoogle Scholar
[22]Vijayaraghavan, T.. A theorem concerning the summability of series by Borel's method. Proc. London Math. Soc. (2) 27 (1928), 316–326.CrossRefGoogle Scholar
[23]Zeller, K. and Beekmann, W.. Theorie der Limitierungsverfahren (Springer-Verlag, 1970).CrossRefGoogle Scholar