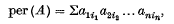Corrigenda
Corrigenda
-
- Published online by Cambridge University Press:
- 24 October 2008, p. 613
-
- Article
-
- You have access
- Export citation
Research Article
On semi-normal lattice rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 613-616
-
- Article
- Export citation
Two notes on spectral synthesis for discrete Abelian groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 617-620
-
- Article
- Export citation
On multilattice groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 621-638
-
- Article
- Export citation
On the fundamental group of an orbit space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 639-646
-
- Article
- Export citation
In-groups, coverings, and imbeddings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 647-656
-
- Article
- Export citation
On embedding 4-manifolds in R7
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 657-658
-
- Article
- Export citation
Unknotting tori in codimension one and spheres in codimension two
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 659-664
-
- Article
- Export citation
The distribution of the sequence {nξ}(n = 0, 1, 2, …)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 665-670
-
- Article
- Export citation
On the least quadratic non-residue
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 671-672
-
- Article
- Export citation
On a functional equation
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 673-677
-
- Article
- Export citation
On the Hausdorff dimension of general Cantor sets
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 679-694
-
- Article
- Export citation
Note on the relations between series equations and integral equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 695-696
-
- Article
- Export citation
On well-quasi-ordering infinite trees
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 697-720
-
- Article
- Export citation
On the degree of smoothness and on singularities in distributions of statistical functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 721-739
-
- Article
- Export citation
Inequalities for permanents and permanental minors
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 741-746
-
- Article
- Export citation
Wald's identity and absorption probabilities for two-dimensional random walks
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 747-762
-
- Article
- Export citation
Gravitational radiation in homogeneous cosmological models with space-sections of constant negative curvature
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 763-765
-
- Article
- Export citation
Diffraction by a perfectly conducting wedge in an anisotropic plasma
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 767-776
-
- Article
- Export citation
On a transformation of use in multiple scattering problems
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 777-779
-
- Article
- Export citation

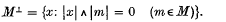
 the normal Stiefel-Whitney class in dimension 3, with integer coefficients (twisted if
the normal Stiefel-Whitney class in dimension 3, with integer coefficients (twisted if