Research Article
On the motion of a flat plate at high speed in a viscous compressible fluid. I. Impulsive motion
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 202-219
-
- Article
- Export citation
The irrotational motion outside a free turbulent boundary
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 220-229
-
- Article
- Export citation
Research Notes
A note on the P-homomorphism in homotopy groups of spheres
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 230-233
-
- Article
- Export citation
Spinor identities
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 234-236
-
- Article
- Export citation
On the converse to a theorem of R. Brauer
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 237-239
-
- Article
- Export citation
The joint distribution for the sizes of the generations in a cascade process
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 240-242
-
- Article
- Export citation
Note on Ehrenfest's equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 243-244
-
- Article
- Export citation
Front matter
PSP volume 51 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 51 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

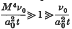 log
log 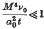 .
.