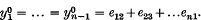Research Article
Laguerre polynomials and derangements
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-214
-
- Article
- Export citation
Families of sets whose pairwise intersections have prescribed cardinals or order types
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 215-221
-
- Article
- Export citation
Valentine convexity in n dimensions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 223-228
-
- Article
- Export citation
The number of solutions of xp = 1 in a finite group
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 229-231
-
- Article
- Export citation
On Baker's inequality for linear forms in logarithms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-248
-
- Article
- Export citation
Continuous singular measures equivalent to their convolution squares
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 249-268
-
- Article
- Export citation
Some more characterizations of Banach spaces containing l1
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 269-276
-
- Article
- Export citation
Harmonic functions on a Riemannian ball
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-282
-
- Article
- Export citation
The departure process from a queueing system
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 283-285
-
- Article
- Export citation
An empirical form of the square root law and the central limit theorem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 287-295
-
- Article
- Export citation
Point processes on spaces of flats and other homogeneous spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 297-314
-
- Article
- Export citation
Deterministic epidemic waves
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-330
-
- Article
- Export citation
Global stability of genetic systems governed by mutation and selection
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 331-336
-
- Article
- Export citation
Spinors in Hilbert space
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 337-347
-
- Article
- Export citation
Complex potential equations II. An application to general relativity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 349-355
-
- Article
- Export citation
On Killing vectors and invariance transformations of the Einstein–Maxwell equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 357-364
-
- Article
- Export citation
New exact results for the defective square lattice
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 365-381
-
- Article
- Export citation
Azumaya algebras and rings with polynomial identity (Addendum)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 383-384
-
- Article
- Export citation
Front matter
PSP volume 80 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 80 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b3
-
- Article
-
- You have access
- Export citation

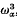 , then one can find
, then one can find 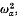 , whose pairwise intersections are arbitrarily prescribed to be either of type ω
, whose pairwise intersections are arbitrarily prescribed to be either of type ω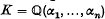 and suppose that
and suppose that 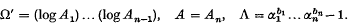
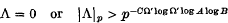
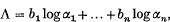
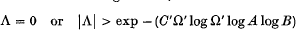
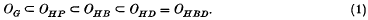
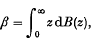
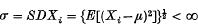
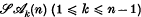 be the space of
be the space of 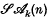 is a topological homogeneous space under the action of the group
is a topological homogeneous space under the action of the group 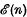 of Euclidean displacements in
of Euclidean displacements in 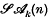 , stationary under
, stationary under 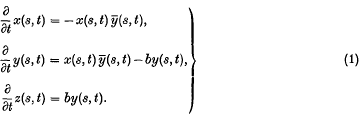
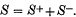
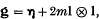
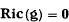
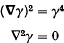
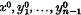 are chosen, the first is diagonal with distinct entries and the others are
are chosen, the first is diagonal with distinct entries and the others are