Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:30:36.996Z Has data issue: false hasContentIssue false
  • English
  • Français

Harmonic functions on a Riemannian ball

Published online by Cambridge University Press:  24 October 2008

Mitsuru Nakai  and
Leo Sario
Mitsuru Nakai
Affiliation:
Nagoya Institute of Technology and University of California, Los Angeles
Leo Sario
Affiliation:
Nagoya Institute of Technology and University of California, Los Angeles
Get access Rights & Permissions [Opens in a new window]

Extract

Consider the classes OHX of noncompact Riemannian manifolds M of dimension N ≥ 2 carrying no non-constant harmonic functions with properties X = P (positive), B (bounded), D (Dirichlet finite), or BD (B and D). Denote by OG the class of parabolic manifolds of dimension N ≥ 2. The following complete string of strict inclusion relations is known:

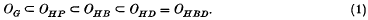
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 80 , Issue 2 , September 1976 , pp. 277 - 282
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hada, D., Sario, L. and Wang, C.N-manifolds carrying bounded but no Dirichlet finite harmonic functions. Nagoya Math. J. 54 (1974), 1–6.CrossRefGoogle Scholar
(2)Müller, C.Spherical Harmonics (Lecture Notes, Berlin, Heidelberg, New York, Springer-Verlag, 1966).CrossRefGoogle Scholar
(3)Nakai, M.A test of Picard's principle for rotation free density. J. Math. Soc. Japan 27 (1975), 412–431.Google Scholar
(4)Sario, L. and Nakai, M.Classification theory of Riemann surfaces (Grundlehren, Berlin, Heidelberg, New York, Springer-Verlag, 1970).CrossRefGoogle Scholar