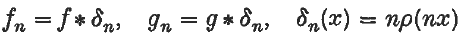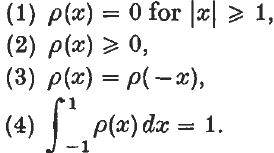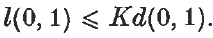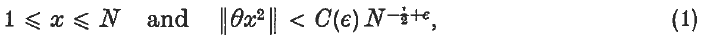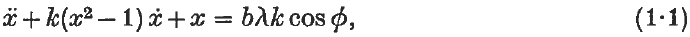Research Article
The combinatorial structure of the Hughes plane. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-139
-
- Article
- Export citation
Local systems and Sylow subgroups in locally finite groups. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 141-160
-
- Article
- Export citation
Regular greatest common divisor of two polynomial matrices
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-165
-
- Article
- Export citation
On the Kunneth formula spectral sequence in equivariant K- theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 167-177
-
- Article
- Export citation
Partitioning the plane into denumerably many sets without repeated distances
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 179-183
-
- Article
- Export citation
On the h-enclosability of spheres†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 185-188
-
- Article
- Export citation
Equivariant integrality theorems for differentiable manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 189-200
-
- Article
- Export citation
The product of the distributions x−r and δ(r−1)(x)
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-204
-
- Article
- Export citation
Arcs with increasing chords
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 205-207
-
- Article
- Export citation
The fractional parts of an additive form
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 209-212
-
- Article
- Export citation
On the non-autonomous van der Pol equation with large parameter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 213-227
-
- Article
- Export citation
Complementary variational principles for a class of differential equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 229-232
-
- Article
- Export citation
Maximum-likelihood estimators with known incidental parameters
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-241
-
- Article
- Export citation
Extension of the Curie principle and constitutive relations for fluids with antisymmetric stress
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 243-251
-
- Article
- Export citation
A steady vortex ring close to Hill's spherical vortex
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 253-284
-
- Article
- Export citation
Coupled fields in inhomogeneous warm plasmas with static pressure gradients. I
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-297
-
- Article
- Export citation
Entropy and simple waves in multidimensional gas flow
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 299-302
-
- Article
- Export citation
Some extremum principles for magnetohydrodynamic flow in conducting pipes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 303-313
-
- Article
- Export citation
Extremum principle for a nonlinear problem in magneto-elasticity
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-318
-
- Article
- Export citation
Peeling and conservation laws in the Born-Infeld theory of electromagnetism
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 319-324
-
- Article
- Export citation

 is a class of groups
is a class of groups