Arcs with increasing chords
Published online by Cambridge University Press: 24 October 2008
Extract
Let f:[0, 1]→R2 be a Jordan arc, and for t, u ∈ [0, 1] let d(t, u) = d(f(t), f(u)) denote the Euclidean length of the chord between f(t) and f(u), and l(t, u) = l(f(t), f(u)) the corresponding arc-length, when this is defined. We say that f has the increasing chord property if d(t2, t3) ≤ d(t1, t4) whenever 0 ≤ t1 ≤ t2 ≤ t3 ≤ t4 ≤ 1. In connexion with a problem in complex analysis, K. Binmore has asked (private communication, see (1)) whether there exists an absolute constant K such that
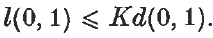 .
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 72 , Issue 2 , September 1972 , pp. 205 - 207
- Copyright
- Copyright © Cambridge Philosophical Society 1972
References
REFERENCES
- 5
- Cited by


