Research Article
Joins of topologies homeomorphic to the rationals
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 256-262
-
- Article
-
- You have access
- Export citation
The volumes of simplices, or, find the penguin
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 263-268
-
- Article
-
- You have access
- Export citation
On the existence of sequences of co-prime pairs of integers
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 84-89
-
- Article
-
- You have access
- Export citation
On the zeroes of profiles
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 424-429
-
- Article
-
- You have access
- Export citation
Symplectic complex bundles over real algebraic four-folds
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 430-437
-
- Article
-
- You have access
- Export citation
Positive semigroups of operators on Banach spaces
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-94
-
- Article
-
- You have access
- Export citation
On discontinuity of l2-angle
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 269-279
-
- Article
-
- You have access
- Export citation
Sufficient conditions for the strong stability of the differential equation [p(D)+f(t)q(D)]y = 0
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 280-299
-
- Article
-
- You have access
- Export citation
Function classes related to Ruscheweyh derivatives
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 438-444
-
- Article
-
- You have access
- Export citation
A construction for Fitting formations II
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 95-102
-
- Article
-
- You have access
- Export citation
The non-emptiness of joint spectral subsets of euclidean n-space
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 300-306
-
- Article
-
- You have access
- Export citation
Boolean near-rings and weak commutativity
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 103-107
-
- Article
-
- You have access
- Export citation
Total chromatic number of graphs of high degree
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 445-452
-
- Article
-
- You have access
- Export citation
On properly separable quotients of strict (LF) Spaces
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-312
-
- Article
-
- You have access
- Export citation
The cohomology ring of a combinatorially aspherical group
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 453-457
-
- Article
-
- You have access
- Export citation
A note on real hypersurfaces of a complex projective space
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 108-113
-
- Article
-
- You have access
- Export citation
Generalized differentiability for a class of nondifferentiable operators with applications to nonsmooth optimization
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 114-132
-
- Article
-
- You have access
- Export citation
Maps into Dynkin diagrams arising from regular monoids
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 313-321
-
- Article
-
- You have access
- Export citation
Walsh-Fourier series with coefficients of generalized bounded variation
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 458-465
-
- Article
-
- You have access
- Export citation
The last problem of Harald Bohr
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 133-152
-
- Article
-
- You have access
- Export citation

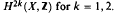 .
. –semigroups is also given.
–semigroups is also given.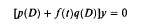 where the continuous function
where the continuous function  is starlike of order α 0 ≤ α < 1. We determine extreme points, inclusion relations, and show how this family acts under various linear operators.
is starlike of order α 0 ≤ α < 1. We determine extreme points, inclusion relations, and show how this family acts under various linear operators.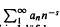 and their order (or Lindelöf) function μ(σ) (= inf{α;
and their order (or Lindelöf) function μ(σ) (= inf{α; with the solution of a previous problem of Bohr; (3) the following answer to the last problem: μ′(σ) can approach − ½, and necessarily μ(σ + μ(σ) + ½) = 0. The characterization of the order functions of ordinary Dirichlet series remains an open question.
with the solution of a previous problem of Bohr; (3) the following answer to the last problem: μ′(σ) can approach − ½, and necessarily μ(σ + μ(σ) + ½) = 0. The characterization of the order functions of ordinary Dirichlet series remains an open question.