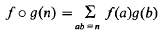Research Article
Semirings with a completely simple additive semigroup
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 257-267
-
- Article
-
- You have access
- Export citation
On tensor product graphs
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 268-273
-
- Article
-
- You have access
- Export citation
Multiple points and Wallman compactifications
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 274-280
-
- Article
-
- You have access
- Export citation
Generalized discrete l-groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-289
-
- Article
-
- You have access
- Export citation
Generalized mean value theorems of the differential calculus
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 290-300
-
- Article
-
- You have access
- Export citation
A class of harmonically convergent sets
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 301-304
-
- Article
-
- You have access
- Export citation
A note on prime radicals of certain group rings
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-306
-
- Article
-
- You have access
- Export citation
Representations of ordered groups with compatible tight Riesz orders
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 307-322
-
- Article
-
- You have access
- Export citation
Second-order Ehrenfeucht games and the deciability of the second-order theory of an equivalence relation
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 323-331
-
- Article
-
- You have access
- Export citation
Changing the scalar multiplication on a vector lattice
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 332-347
-
- Article
-
- You have access
- Export citation
On a subgroup of the group of multiplicative arithmetic functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 348-358
-
- Article
-
- You have access
- Export citation
General rings of functions
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 359-365
-
- Article
-
- You have access
- Export citation
Closed subalgebras of homogeneous Banach algebras
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-376
-
- Article
-
- You have access
- Export citation
Regular graphs and stability
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 377-384
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 20 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 20 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation