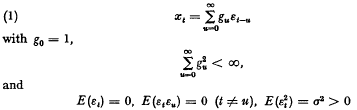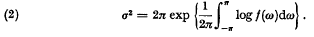Research Article
Right invariant integrals on locally compact semigroups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 273-286
-
- Article
-
- You have access
- Export citation
Comments on the preceding paper of Michael's
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-288
-
- Article
-
- You have access
- Export citation
A note on Green's Theorem
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 289-292
-
- Article
-
- You have access
- Export citation
Averaging operators on the ring of continuous functions on a compact space1
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 293-298
-
- Article
-
- You have access
- Export citation
On the radical of a category
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 299-307
-
- Article
-
- You have access
- Export citation
Projectivities in finite groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 308-326
-
- Article
-
- You have access
- Export citation
A generalization of z!
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-341
-
- Article
-
- You have access
- Export citation
Computation of the generalised factorial function
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 342-346
-
- Article
-
- You have access
- Export citation
Stochastic non-linear programming
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 347-353
-
- Article
-
- You have access
- Export citation
Doppler broadened contour functions in the complex domain
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 354-362
-
- Article
-
- You have access
- Export citation
Asymptotic properties of least-squares estimates of parameters of the spectrum of a stationary non-deterministic time-series
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-384
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 4 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 4 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 of continuous real-valued functions on ς with compact supports. If ς has the property: (A) for each pair of compact sets
of continuous real-valued functions on ς with compact supports. If ς has the property: (A) for each pair of compact sets 
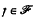 and a ∈ S, the function
and a ∈ S, the function 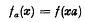
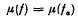
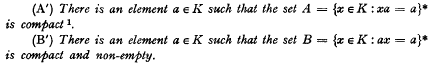
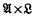 such that
such that  supports a measure
supports a measure 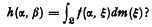
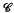 and
and 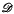 and an additive functor
and an additive functor 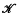 of
of 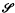 (G) of subnormal subgroups of group G have been considered by various authors, see for example Barnes [1] and Tamaschke [2].
(G) of subnormal subgroups of group G have been considered by various authors, see for example Barnes [1] and Tamaschke [2].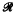 (z) < 0, (z: k)! is analytic in both variables, and that F(z) may be expressed in the form F(z) = πz/(z: k)!(—z: k)!
(z) < 0, (z: k)! is analytic in both variables, and that F(z) may be expressed in the form F(z) = πz/(z: k)!(—z: k)!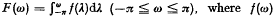 is the spectral density function. It is well known that {x
is the spectral density function. It is well known that {x