Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Conlon, S.B
1968.
Relative components of representations.
Journal of Algebra,
Vol. 8,
Issue. 4,
p.
478.
Roberts, Leslie G.
1969.
𝐾₁ of some abelian categories.
Transactions of the American Mathematical Society,
Vol. 138,
Issue. 0,
p.
377.
Tsalenko, M. S.
and
Shul’geifer, E. G.
1971.
Progress in Mathematics.
p.
3.
Mitchell, Barry
1972.
Rings with several objects.
Advances in Mathematics,
Vol. 8,
Issue. 1,
p.
1.
Tarafdar, E.
1972.
Improjective operators and ideals in a category of Banach spaces.
Journal of the Australian Mathematical Society,
Vol. 14,
Issue. 3,
p.
274.
Beck, István
1978.
On modules whose endomorphism ring is local.
Israel Journal of Mathematics,
Vol. 29,
Issue. 4,
p.
393.
Quebbemann, H.-G
Scharlau, W
and
Schulte, M
1979.
Quadratic and hermitian forms in additive and abelian categories.
Journal of Algebra,
Vol. 59,
Issue. 2,
p.
264.
Kelly, Max
1979.
Saunders Mac Lane Selected Papers.
p.
527.
Ringel, Claus Michael
1980.
Representation Theory I.
Vol. 831,
Issue. ,
p.
104.
Street, Ross
1995.
Ideals, radicals, and structure of additive categories.
Applied Categorical Structures,
Vol. 3,
Issue. 2,
p.
139.
Kasch, Friedrich
1995.
Verallgemeinerung der Sätze von Johnson und Utumi auf Hom.
Periodica Mathematica Hungarica,
Vol. 31,
Issue. 3,
p.
209.
Sun, Shu-Hao
and
Dhillon, Ajneet
1997.
Prime spectra of additive categories (I).
Journal of Pure and Applied Algebra,
Vol. 122,
Issue. 1-2,
p.
135.
Simson, Daniel
2000.
An Artin Problem for Division Ring Extensions and the Pure Semisimplicity Conjecture, II.
Journal of Algebra,
Vol. 227,
Issue. 2,
p.
670.
Jannsen, Uwe
2000.
The Arithmetic and Geometry of Algebraic Cycles.
p.
225.
Nowak, Sebastian
and
Simson, Daniel
2002.
LOCALLY DYNKIN QUIVERS AND HEREDITARY COALGEBRAS WHOSE LEFT COMODULES ARE DIRECT SUMS OF FINITE DIMENSIONAL COMODULES.
Communications in Algebra,
Vol. 30,
Issue. 1,
p.
455.
Borne, Niels
2006.
Cohomology of G-sheaves in positive characteristic.
Advances in Mathematics,
Vol. 201,
Issue. 2,
p.
454.
Abyzov, A. N.
and
Tuganbaev, A. A.
2012.
Homomorphisms close to regular and their applications.
Journal of Mathematical Sciences,
Vol. 183,
Issue. 3,
p.
275.
Krause, Henning
2012.
Report on locally finite triangulated categories.
Journal of K-theory,
Vol. 9,
Issue. 3,
p.
421.
Krause, Henning
2015.
Krull–Schmidt categories and projective covers.
Expositiones Mathematicae,
Vol. 33,
Issue. 4,
p.
535.
Wildeshaus, Jörg
2015.
On the interior motive of certain Shimura varieties: the case of Picard surfaces.
Manuscripta Mathematica,
Vol. 148,
Issue. 3-4,
p.
351.
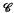 and
and 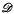 and an additive functor T:
and an additive functor T: 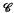 →
→ 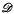 , a criterion for T (supposed surjective) to be complete was given in terms of the kernel
, a criterion for T (supposed surjective) to be complete was given in terms of the kernel 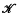 of T: this was that for each object A of
of T: this was that for each object A of 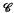 the ideal
the ideal 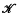 A should be containded in the (Jacobson) radical of
A should be containded in the (Jacobson) radical of 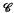 A. (The meaning of this notation and nomemclature is recalled in § 2 below). The question arises whether in any additive category
A. (The meaning of this notation and nomemclature is recalled in § 2 below). The question arises whether in any additive category 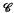 there is a greatest ideal
there is a greatest ideal 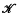 with this property, so that the canonical functor T:
with this property, so that the canonical functor T: 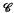 →
→ 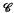 /
/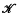 is in some sense the coarsest that faithfully represents the objects (but not the maps) of
is in some sense the coarsest that faithfully represents the objects (but not the maps) of 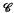 .
.