Research Article
Regularity of spherical means and localization of spherical harmonic expansions
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-297
-
- Article
-
- You have access
- Export citation
Digraphs with eulerian chains
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 298-303
-
- Article
-
- You have access
- Export citation
Numerical ranges in locally M-convex algebras. I
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 304-316
-
- Article
-
- You have access
- Export citation
Inscribed centers, reflexivity, and some applications
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 317-324
-
- Article
-
- You have access
- Export citation
Corrigenda
Twenty-step algorithm for determining the asymptotic number of trees of various species: corrigenda
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, p. 325
-
- Article
-
- You have access
- Export citation
Research Article
On non-uniform and global descriptions of the rate of convergence of Asymptotic expansions in the central limit theorem
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 326-335
-
- Article
-
- You have access
- Export citation
On a problem of Niederreiter and Robinson about finite fields
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 336-338
-
- Article
-
- You have access
- Export citation
On the number of p-blocks of a p-soluble group
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 339-342
-
- Article
-
- You have access
- Export citation
On the number of normal subgroups of an uncountable group
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-351
-
- Article
-
- You have access
- Export citation
Products of locally finite groups with min-p
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 352-360
-
- Article
-
- You have access
- Export citation
A class of finite groups having nilpotent injectors
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 361-365
-
- Article
-
- You have access
- Export citation
Representations of minimally almost periodic groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-375
-
- Article
-
- You have access
- Export citation
L1-convergence of Fourier series
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 376-390
-
- Article
-
- You have access
- Export citation
Growth of solutions of weakly coupled parabolic systems and Laplace's equation
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 391-403
-
- Article
-
- You have access
- Export citation
Critical associated metrics on contact manifolds. II
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 404-410
-
- Article
-
- You have access
- Export citation
Primitive ideals with bounded approximate units in L1-algebras of exponential lie groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 411-420
-
- Article
-
- You have access
- Export citation
Index
Index
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 421-422
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 41 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 41 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

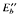 of a unital infrabarrelled l.m.c.
of a unital infrabarrelled l.m.c. 
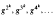 for some positive integer
for some positive integer 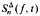 and establish its
and establish its 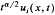 exceeds 1. Related results for Poisson integrals on a half-space are also described, some applications are given, and interesting comparisons emerge.
exceeds 1. Related results for Poisson integrals on a half-space are also described, some applications are given, and interesting comparisons emerge.