Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T08:45:16.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Numerical ranges in locally M-convex algebras. I

Part of: Topological algebras, normed rings and algebras, Banach algebras Topological (rings and) algebras with an involution

Published online by Cambridge University Press:  09 April 2009

Thanassis Chryssakis
Thanassis Chryssakis
Affiliation:
Mathematical Institute, University of Athens, 57, Solonos Street, Athens 10679, Greece
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The bidual 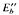of a unital infrabarrelled l.m.c. C* algebra E, equipped with the bidual topology and the regualr Arens product, is always an l.m.c. C*-algebra. On the other hand, a unital l.m.c. *-algebra E has the C*-property if and only if every self-adjoint element x of E is strongly hermitian (x has real numerical range), or the sets of normalized states and normalized continuous positive linear forms of E coincide. Finally, every unital cpmplete l.m.c. C* algebra satisfying, locally, the property ‘the extreme points are dense in that set of continuous positive linear forms” (antiliminal algebra) has the complexes as its only normal elements.

Keywords

numerical rangenormalized statesI.m.c. *-algebraI.m.c. C*-akgebra.

MSC classification

Secondary: 46H99: None of the above, but in this section 46K99: None of the above, but in this section
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 41 , Issue 3 , December 1986 , pp. 304 - 316
Copyright
Copyright © Australian Mathematical Society 1986

References

Berberian, S. (1974), Lectures in functional analysis and operator theory (Springer-Verlag, New York).CrossRefGoogle Scholar
Bonsall, F. and Duncan, J. (1971), Numerical ranges of operators on normed spaces and of elements of normed algebras (London Math. Soc. Lecture Notes, Ser. 2, Cambridge University Press).CrossRefGoogle Scholar
Bratteli, O. and Robinson, D. (1979), Operator algebras and quantum statistical mechanisms I (Springer-Verlag, Berlin).Google Scholar
Brooks, R. M. (1967), ‘On locally m-convex *-algebras’, Pacific J. Math. 23, 5–23.CrossRefGoogle Scholar
Fragoulopoulou, M. (1983), ‘Spaces of representations and enveloping l.m.c. *-algebras’, Pacific Math. 95, 61–73.CrossRefGoogle Scholar
Giles, J. and Koehler, D. (1973), ‘On numerical ranges of elements of locally m-convex algebras’, Pacific J. Math. 49, 79–81.Google Scholar
Gulick, S. L. (1966), ‘The bidual of a locally multiplicatively-convex algebra’, Pacific J. Math. 17, 71–76.Google Scholar
Horváth, J. (1966), Topological vector spaces and distributions (Addison-Wesely, Reading, Mass.).Google Scholar
Inoue, A. (1971), ‘Locally C*-algebras’, Mem Fac. of Sci. Kyushu Univ. 25, 197–235.Google Scholar
Lummer, G. (1961), ‘Semi-inner product spaces’, Trans. Amer. Math. Soc. 100, 41–43.Google Scholar
Mallios, A. (1986), Topological algebras: selected topics (North-Holland, Amsterdam).Google Scholar
Michael, E. (1952), Locally multiplicatively convex topological algebras, (Men. Amer. Math. Soc., No. 11).CrossRefGoogle Scholar
Sims, B. (1971), ‘A characterization of Banach *-algebras by numerical range’, Bull. Austral. Math. Soc. 4, 193–200.CrossRefGoogle Scholar
Srinivasacharyulu, K. (1974), ‘Remarks on Banach algebras’, Bull. Soc. Sci. de Liège, 43, 523–525.Google Scholar
Treves, F. (1967), Topological vector spaces, distributions and kernels (Academic Press, New York).Google Scholar
Wenjen, Ch. (1968), ‘A remark on a problem of M. A. Naimark’, Proc. Japan Acad. 44, 651–655.Google Scholar
Yood, B. (1960), ‘Faithful *-representations of normed algebras’, Pacific J. Math. 10, 346–363.CrossRefGoogle Scholar