Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T09:09:16.128Z Has data issue: false hasContentIssue false
  • English
  • Français

SYMMETRIC GRAPHS WITH 2-ARC TRANSITIVE QUOTIENTS

Part of: Graph theory Algebraic combinatorics

Published online by Cambridge University Press:  17 April 2014

GUANGJUN XU  and
SANMING ZHOU
GUANGJUN XU*
Affiliation:
Department of Mathematics and Statistics, The University of Melbourne, Parkville, VIC 3010, Australia email [email protected]
SANMING ZHOU
Affiliation:
Department of Mathematics and Statistics, The University of Melbourne, Parkville, VIC 3010, Australia email [email protected]
*
✉
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A graph 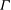$\Gamma $ is 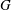$G$-symmetric if 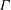$\Gamma $ admits 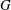$G$ as a group of automorphisms acting transitively on the set of vertices and the set of arcs of 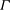$\Gamma $, where an arc is an ordered pair of adjacent vertices. In the case when 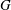$G$ is imprimitive on 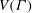$V(\Gamma )$, namely when 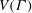$V(\Gamma )$ admits a nontrivial 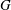$G$-invariant partition 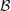${\mathcal{B}}$, the quotient graph 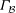$\Gamma _{\mathcal{B}}$ of 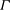$\Gamma $ with respect to 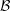${\mathcal{B}}$ is always 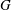$G$-symmetric and sometimes even 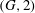$(G, 2)$-arc transitive. 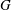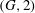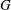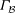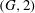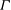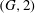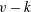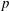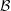(A $G$-symmetric graph is $(G, 2)$-arc transitive if $G$ is transitive on the set of oriented paths of length two.) In this paper we obtain necessary conditions for $\Gamma _{{\mathcal{B}}}$ to be $(G, 2)$-arc transitive (regardless of whether $\Gamma $ is $(G, 2)$-arc transitive) in the case when $v-k$ is an odd prime $p$, where $v$ is the block size of ${\mathcal{B}}$ and 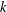$k$ is the number of vertices in a block having neighbours in a fixed adjacent block. These conditions are given in terms of 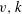$v, k$ and two other parameters with respect to 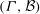$(\Gamma , {\mathcal{B}})$ together with a certain 2-point transitive block design induced by 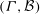$(\Gamma , {\mathcal{B}})$. We prove further that if 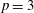$p=3$ or 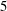$5$ then these necessary conditions are essentially sufficient for 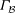$\Gamma _{{\mathcal{B}}}$ to be 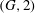$(G, 2)$-arc transitive.

Keywords

symmetric grapharc-transitive graph2-arc transitive graph3-arc graphtransitive block design

MSC classification

Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 05E18: Group actions on combinatorial structures
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 96 , Issue 2 , April 2014 , pp. 275 - 288
Copyright
Copyright © 2014 Australian Mathematical Publishing Association Inc. 

References

Beth, T., Jungnickel, D. and Lenz, H., Design Theory, 2nd edn (Cambridge University Press, Cambridge, 1999).Google Scholar
Biggs, N. L., Algebraic Graph Theory, 2nd edn (Cambridge Mathematical Library, Cambridge University Press, Cambridge, 1993).Google Scholar
Broersma, H. J. and Hoede, C., ‘Path graphs’, J. Graph Theory 13 (1989), 427–444.CrossRefGoogle Scholar
Colbourn, C. J. and Dinitz, J. H., Handbook of Combinatorial Designs, 2nd edn (CRC Press, Boca Raton, 2007).Google Scholar
Dixon, J. D. and Mortimer, B., Permutation Groups (Springer, New York, 1996).CrossRefGoogle Scholar
Gardiner, A. and Praeger, C. E., ‘A geometrical approach to imprimitive graphs’, Proc. Lond. Math. Soc. (3) 71 (1995), 524–546.CrossRefGoogle Scholar
Iranmanesh, M. A., Praeger, C. E. and Zhou, S., ‘Finite symmetric graphs with two-arc transitive quotients’, J. Combin. Theory Ser. B 94 (2005), 79–99.CrossRefGoogle Scholar
Jia, B., Lu, Z. and Wang, G. X., ‘A class of symmetric graphs with 2-arc transitive quotients’, J. Graph Theory 65 (2010), 232–245.CrossRefGoogle Scholar
Kantor, W. M., ‘Classification of 2-transitive symmetric designs’, Graphs Combin. 1(2) (1985), 165–166.CrossRefGoogle Scholar
Li, C. H., Praeger, C. E. and Zhou, S., ‘A class of finite symmetric graphs with 2-arc transitive quotients’, Math. Proc. Cambridge Philos. Soc. 129 (2000), 19–34.CrossRefGoogle Scholar
Li, C. H., Praeger, C. E. and Zhou, S., ‘Imprimitive symmetric graphs with cyclic blocks’, Eur. J. Combin. 31 (2010), 362–367.CrossRefGoogle Scholar
Lu, Z. and Zhou, S., ‘Finite symmetric graphs with 2-arc transitive quotients (II)’, J. Graph Theory 56 (2007), 167–193.CrossRefGoogle Scholar
Xu, G. and Zhou, S., ‘Solution to a question on a family of imprimitive symmetric graphs’, Bull. Aust. Math. Soc. 82 (2010), 79–83.CrossRefGoogle Scholar
Zhou, S., ‘Constructing a class of symmetric graphs’, Eur. J. Combin. 23 (2002), 741–760.CrossRefGoogle Scholar
Zhou, S., ‘Symmetric graphs and flag graphs’, Monatsh. Math. 139 (2003), 69–81.CrossRefGoogle Scholar
Zhou, S., ‘Almost covers of 2-arc transitive graphs’, Combinatorica 24 (2004), 731–745; [Erratum: 27 (2007), 745–746].CrossRefGoogle Scholar
Zhou, S., ‘On a class of finite symmetric graphs’, Eur. J. Combin. 29 (2008), 630–640.CrossRefGoogle Scholar