Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-12-02T20:58:03.386Z Has data issue: false hasContentIssue false
  • English
  • Français

Some Fourier division problems

Published online by Cambridge University Press:  09 April 2009

R. E. Edwards
R. E. Edwards
Affiliation:
Department of Mathematics Institute of Advanced Studies, ANU
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T denote the circle group, C the set of continuous complex-valued functions on T, and A the set of f ∈ C having absolutely convergent Fourier series:

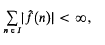
I standing for the set of integers.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 12 , Issue 2 , May 1971 , pp. 167 - 186
Copyright
Copyright © Australian Mathematical Society 1971

References

[1]Shilov, G. E., ‘On the Fourier coefficients of a class of continuous functions’, (In Russian.) Doklady Akad. Nauk 35 (1942), 3–7.Google Scholar
[2I, II]Bary, N., A Treatise on Trigonometric Series. Vols. I, II (Pergamon Press, Oxford, 1964).Google Scholar
[3I, II]Edwards, R. E., Fourier Series: A Modern Introduction (Vols. I, II. Holt, Rinehart & Winston, Inc., New York, 1967, 1968).Google Scholar
[4]Zygmund, A., Trigonometric Series, Vol. I (Cambridge University Press, 1959).Google Scholar
[5]Edwards, R. E. and Hewitt, E., ‘Pointwise limits for sequences of convolution operators’, Acta Math. 113 (1965), 181–218.CrossRefGoogle Scholar
[6]Edwards, R. E., Functional Analysis: Theory and Applications (Holt, Rinehart and Winston, Inc., New York, 1965).Google Scholar
[7]Katznelson, Y., An Introduction to Harmonic Analysis (John Wiley and Sons, Inc., New York, 1968).Google Scholar