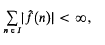Research Article
On non-cross varieties of groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-144
-
- Article
-
- You have access
- Export citation
Subgroups of free solvable groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-160
-
- Article
-
- You have access
- Export citation
On lattices of varieties of metabelian groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 161-166
-
- Article
-
- You have access
- Export citation
Some Fourier division problems
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 167-186
-
- Article
-
- You have access
- Export citation
On the equivalence of cancellative extensions of commutative cancellative semigroups by groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-192
-
- Article
-
- You have access
- Export citation
The category of representations of a completely 0-simple semigroup
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 193-210
-
- Article
-
- You have access
- Export citation
Stone's theorem and completeness of orthogonal systems
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 211-223
-
- Article
-
- You have access
- Export citation
Non-negative values of quadratic forms
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 224-238
-
- Article
-
- You have access
- Export citation
Remarks about the digits of integers
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 239-241
-
- Article
-
- You have access
- Export citation
An inner orthogonality of Hadamard matrices
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 242-248
-
- Article
-
- You have access
- Export citation
On the cohomology of local groups
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. 249-255
-
- Article
-
- You have access
- Export citation
Corrigendum
Corrigendum
-
- Published online by Cambridge University Press:
- 09 April 2009, p. 256
-
- Article
-
- You have access
- Export citation
Front matter
JAZ volume 12 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JAZ volume 12 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 09 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation