Research Article
The degrees below a 1-generic degree < 0′
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 770-777
-
- Article
- Export citation
A simple solution to Friedman's fourth problem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 778-784
-
- Article
- Export citation
Inverse topological systems and compactness in abstract model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 785-794
-
- Article
- Export citation
À l'ouest d'Éden
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 795-816
-
- Article
- Export citation
Reviews
Anna R. Bruss and Albert R. Meyer. On time-space classes and their relation to the theory of real addition. Theoretical computer science, vol. 11 (1980), pp. 59–69. - Leonard Berman. The complexity of logical theories. Theoretical computer science, pp. 71–77. - Hugo Volger. Turing machines with linear alternation, theories of bounded concatenation and the decision problem of first order theories. Theoretical computer science, vol. 23 (1983), pp. 333–337.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 817-818
-
- Article
- Export citation
Saul A. Kripke. Wittgenstein on rules and private language. An elementary exposition. Harvard University Press, Cambridge, Mass., 1982, x + 150 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 819-821
-
- Article
- Export citation
Leonard Linsky. Oblique contexts. The University of Chicago Press, Chicago and London1983, xxxvii + 175 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 821-822
-
- Article
- Export citation
H. Jerome Keisler. An infinitesimal approach to stochastic analysis. Memoirs of the American Mathematical Society, no. 297. American Mathematical Society, Providence1984, x + 184 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 822-824
-
- Article
- Export citation
Dov M. Gabbay. Semantical investigations in Heyting's intuitionistic logic. Synthese library, vol. 148. D. Reidel Publishing Company, Dordrecht, Boston, and London, 1981, x + 287 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 824
-
- Article
- Export citation
G. E. Hughes and M. J. Cresswell. A companion to modal logic. Methuen, London 1984 and New York 1985, xvii + 203 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 824-826
-
- Article
- Export citation
Dirk van Dalen. Logic and structure. Universitext. Springer-Verlag, Berlin, Heidelberg, and New York, 1980, ix + 172 pp. - Dirk van Dalen. Logic and structure. Second edition of the preceding. Universitext. Springer-Verlag, Berlin etc. 1983, x + 207 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 826-827
-
- Article
- Export citation
Ermanno Bencivenga. Il primo libro di logica. Introduzione ai metodi delta logica contemporanea. Serie di logica matematica. Boringhieri, Turin1984, 228 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 827
-
- Article
- Export citation
Ú. L. Éršov and É. A. Palútin. Matématičéskaá logika (Mathematical logic). “Nauka,” Moscow1979, 320 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 827-829
-
- Article
- Export citation
Yu. L. Ershov and E. A. Palyutin. Mathematical logic. Revised English translation by Vladimir Shokurov of the preceding. Mir Publishers, Moscow1984, 303 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 829
-
- Article
- Export citation
Yu. I. Manin. A course in mathematical logic. Translated from the Russian by Neal Koblitz. Graduate texts in mathematics, vol. 53. Springer-Verlag, New York, Heidelberg, and Berlin, 1977, xiii + 286 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 829-830
-
- Article
- Export citation
Abram Aronovich Stolyar. Introduction to elementary mathematical logic. English translation edited by Elliot; Mendelson of Eléméntarnoé vvédénié v matématičéskuú logiku. The MIT Press, Cambridge, Mass., and London, © 1970, pub. 1971, and Dover Publications, New York 1983, vii + 209 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 830-831
-
- Article
- Export citation
Meeting Report
Meeting of the Association for Symbolic Logic, Stanford, California, 1985
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 832-862
-
- Article
- Export citation
Other
Notices
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 863-864
-
- Article
- Export citation
Front matter
JSL volume 51 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JSL volume 51 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation

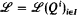 , generated by a set of quantifiers
, generated by a set of quantifiers 
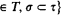 is an inverse topological system whose bonding mappings
is an inverse topological system whose bonding mappings 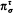 are naturally determined by the reduct operation on structures. We relate the compactness of
are naturally determined by the reduct operation on structures. We relate the compactness of 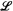 to the topological properties of
to the topological properties of