Research Article
A Gentzen- or Beth-type system, a practical decision procedure and a constructive completeness proof for the counterfactual logics VC and VCS
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-20
-
- Article
- Export citation
Indiscernibles and decidable models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 21-32
-
- Article
- Export citation
On the standard part of nonstandard models of set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 33-38
-
- Article
- Export citation
On generic extensions without the axiom of choice1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 39-52
-
- Article
- Export citation
Logic of reduced power structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 53-59
-
- Article
- Export citation
Post-scriptum à “Théories instables”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 60-62
-
- Article
- Export citation
Choice principles, the bar rule and autonomously iterated comprehension schemes in analysis
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 63-70
-
- Article
- Export citation
Son of George and V = L
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 71-77
-
- Article
- Export citation
Core models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 78-90
-
- Article
- Export citation
Real functions on the family of all well-ordered subsets of a partially ordered set1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 91-96
-
- Article
- Export citation
Antitheses in systems of relevant implication
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 97-99
-
- Article
- Export citation
Maximality in effective topology
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 100-112
-
- Article
- Export citation
Proper classes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 113-139
-
- Article
- Export citation
QE rings in characteristic pn
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 140-162
-
- Article
- Export citation
A note on finitely generated models
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 163-166
-
- Article
- Export citation
The existence of countable totally nonconstructive extensions of the countable atomless Boolean algebra
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 167-170
-
- Article
- Export citation
Omitting types, type spectrums, and decidability1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 171-181
-
- Article
- Export citation
The optimality of induction as an axiomatization of arithmetic1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 182-184
-
- Article
- Export citation
Hyperhypersimple supersets in admissible recursion theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 185-192
-
- Article
- Export citation
Decision problem for separated distributive lattices
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 193-196
-
- Article
- Export citation

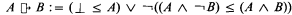 (if
(if 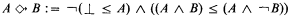 (if
(if  and
and  are two counterfactual conditional operators. (
are two counterfactual conditional operators. (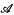
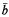 tels que
tels que 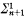 -AC) is a conservative extension of (
-AC) is a conservative extension of (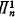 -CA)
-CA) -sentences where
-sentences where 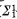 -DC) + (BR) is a conservative extension of (
-DC) + (BR) is a conservative extension of (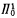 -CA)
-CA)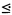 defined as follows:
defined as follows: 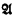 of the countable atomless Boolean algebra
of the countable atomless Boolean algebra  such that
such that 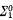 . If
. If 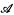 is an
is an 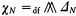 .
.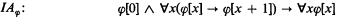
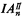 be the schema
be the schema  ); similarly for
); similarly for 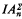 . Each instance of
. Each instance of 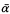 of an instance
of an instance 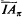
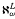 ) of hh-simple
) of hh-simple 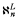 for any
for any