Research Article
Ordinals connected with formal theories for transfinitely iterated inductive definitions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 161-182
-
- Article
- Export citation
Toward model theory through recursive saturation1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 183-206
-
- Article
- Export citation
Formalisations of further ℵ0-valued Łukasiewicz propositional calculi
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 207-210
-
- Article
- Export citation
An incomplete nonnormal extension of S3
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 211-212
-
- Article
- Export citation
A type-free Gödel interpretation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 213-227
-
- Article
- Export citation
Some relations between classical and constructive mathematics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 228-246
-
- Article
- Export citation
Some anomalies in Fitch's system QD
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 247-249
-
- Article
- Export citation
The ℵ1-categoricity of strictly upper triangular matrix rings over algebraically closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 250-259
-
- Article
- Export citation
Simple and hyperhypersimple vector spaces1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 260-269
-
- Article
- Export citation
The uniform regular set theorem in α-recursion theory1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 270-279
-
- Article
- Export citation
Diagonalization in degree constructions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 280-283
-
- Article
- Export citation
An ideal game
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 284-292
-
- Article
- Export citation
Major subspaces of recursively enumerable vector spaces1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 293-303
-
- Article
- Export citation
Ideal models and some not so ideal problems in the model theory of L(Q)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 304-321
-
- Article
- Export citation
Nowhere simple sets and the lattice of recursively enumerable sets1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 322-330
-
- Article
- Export citation
An inelastic model with indiscernibles
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 331-334
-
- Article
- Export citation
Three universal representations of recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 335-351
-
- Article
- Export citation
Meeting Report
Meeting of the Association for Symbolic Logic, Campinas, Brazil, 1976
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 352-364
-
- Article
- Export citation
Annual meeting of the Association for Symbolic Logic, Saint Louis, 1977
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 365-372
-
- Article
- Export citation
Reviews
Peter Aczel. Quantifiers, games and inductive definitions. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 1–14. - Kit Fine. Some connections between elementary and modal logic. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 15–31. - Bengt Hansson and Peter Gärdenfors. Filtations and the finite frame property in Boolean semantics. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 32–39. - Jaakko Hintikka and Veikko Rantala. Systematizing definability theory. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 40–62. - Herman Ruge Jervell. Conservative endextensions and the quantifier ‘there exist uncountably many.’Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 63–80. - Per Martin-Löf. About models for intuitionistic type theories and the notion of definitional equality. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 81–109. - Henrik Sahlqvist. Completeness and correspondence in the first and second order semantics for modal logic. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 110–143. - Arto Salomaa. On some decidability problems concerning developmental languages. Proceedings of the Third Scandinavian Logic Symposium, edited by Stig Kanger, Studies in logic and the foundations of mathematics, vol. 82, North-Holland Publishing Company, Amsterdam and Oxford, and American Elsevier Publishing Company, Inc., New York, 1975, pp. 144–153.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 373-376
-
- Article
- Export citation

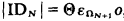 , where ID
, where ID [X,
[X,
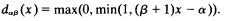
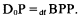
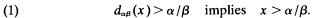
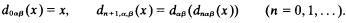
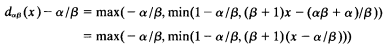
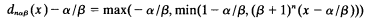
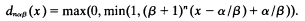
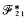 (see [1]) can also be applied to Fitch's system
(see [1]) can also be applied to Fitch's system 
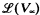 be the lattice consisting of the recursively enumerable (r.e.) subspaces of
be the lattice consisting of the recursively enumerable (r.e.) subspaces of 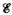 of r.e. sets to
of r.e. sets to 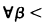
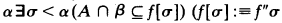 is the image of the set σ under
is the image of the set σ under 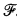 . By fully effective we mean that
. By fully effective we mean that 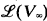 , the lattice of r.e. subspaces of
, the lattice of r.e. subspaces of 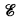 the lattice of r.e. sets and
the lattice of r.e. sets and 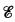 and
and 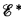 of r.e. sets and r.e. sets modulo finite sets respectively. (This lattice theoretic viewpoint was introduced by Myhill [3].) Key roles in both areas have been played by the lattice of r.e. supersets,
of r.e. sets and r.e. sets modulo finite sets respectively. (This lattice theoretic viewpoint was introduced by Myhill [3].) Key roles in both areas have been played by the lattice of r.e. supersets, 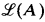 , of an r.e. set
, of an r.e. set 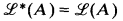 modulo finite sets) and more recently by the group of automorphisms of
modulo finite sets) and more recently by the group of automorphisms of 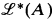 ) being a Boolean algebra. Indeed Lachlan even tells us which Boolean algebras appear as
) being a Boolean algebra. Indeed Lachlan even tells us which Boolean algebras appear as 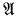 and
and 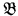 be L-structures such that
be L-structures such that 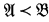 ,
, 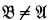 and
and 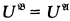 . Under what conditions will
. Under what conditions will