Article contents
The uniform regular set theorem in α-recursion theory1
Published online by Cambridge University Press: 12 March 2014
Extract
Several new features arise in the generalization of recursion theory on ω to recursion theory on admissible ordinals α, thus making α-recursion theory an interesting theory. One of these is the appearance of irregular sets. A subset A of α is called regular (over α), if we have for all β < α that A ∩ B ∈ Lα, otherwise A is called irregular (over α). So in the special case of ordinary recursion theory (α = ω) every subset of α is regular, but if α is not a cardinal of L we find constructible sets A ⊆ α which are irregular. The notion of regularity becomes essential, if we deal with α-recursively enumerable (α-r.e.) sets in priority constructions (α-r.e. is defined as Σ1 over Lα). The typical situation occurring there is that an α-r.e. set A is enumerated during some construction in which one tries to satisfy certain requirements. Often this construction succeeds only if we can insure that every initial segment A ∩ β of A is completely enumerated at some stage before α. This calls for making sure that A is regular because due to the admissibility of α an α-r.e. set A is regular iff for every (or equivalently for one) enumeration f of A (f is an enumeration of A iff f: α → A is α-recursive, total, 1-1 and onto) we have that 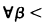
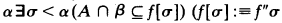 is the image of the set σ under f).
is the image of the set σ under f).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
Footnotes
This paper was written at M.I.T., where the author was supported by the Deutsche Forschungsgemeinschaft, Bonn.
References
REFERENCES
- 2
- Cited by


