We consider a set generic over the arithmetic sets. A subset A of the natural numbers is called n-generic if it is Cohen-generic for n-quantifier arithmetic. This is equivalent to saying that for every 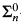 -set of strings S, there is a string σ ⊂ A such that σ ∈ S or no extension of σ is in S. By degree we mean Turing degree (of unsolvability). We call a degree n-generic if it has an n-generic representative. For a degree a, let D(≤ a) denote the set of degrees which are recursive in a.
-set of strings S, there is a string σ ⊂ A such that σ ∈ S or no extension of σ is in S. By degree we mean Turing degree (of unsolvability). We call a degree n-generic if it has an n-generic representative. For a degree a, let D(≤ a) denote the set of degrees which are recursive in a.
We say a is a strong minimal cover of g if every degree strictly below a is less than or equal to g. In this paper we show that there are a 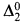 degree a and a 1-generic degree g < a such that a is a strong minimal cover of g. This easily implies that there is a 1-generic degree without the cupping property. Jockusch [7] showed that every 2-generic degree has the cupping property. Slaman and Steel [17] and independently Cooper [3] showed that there are recursively enumerable degrees a and b < a such that no degree c < a joins b above a. Take a 1-generic degree g below b. Then g does not have the cupping property.
degree a and a 1-generic degree g < a such that a is a strong minimal cover of g. This easily implies that there is a 1-generic degree without the cupping property. Jockusch [7] showed that every 2-generic degree has the cupping property. Slaman and Steel [17] and independently Cooper [3] showed that there are recursively enumerable degrees a and b < a such that no degree c < a joins b above a. Take a 1-generic degree g below b. Then g does not have the cupping property.

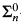 -set of strings
-set of strings 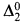 degree
degree  allowing parameters. The purpose of this paper is to explore the concepts of located and weakly located subsets of a compact separable metric space in the context of subsystems of second order arithmetic such as RCA
allowing parameters. The purpose of this paper is to explore the concepts of located and weakly located subsets of a compact separable metric space in the context of subsystems of second order arithmetic such as RCA