Whenever particular ordinals are used as tools in a proof or a definition, it is necessary to find a way of representing them. If the ordinals are sufficiently small, there is a standard way (e.g. Cantor normal forms for ordinals less than ε0); in general, representations are often found by using functions on initial segments of the ordinals: Each term which can be obtained from by applications of a function symbol is regarded as a notation for the ordinal obtained by the same applications of the function f to the ordinal 0. In this way, f provides representations for all the ordinals in Clf(0), the closure set of f (se e §1). (For an introduction to and development of this principle, see Feferman [F1]; and for a discussion of the significance of such representations in proof theory, see Kreisel [K1, pp. 22–34].) Thus it is natural to ask whether there are connections between frequently encountered properties of ordinal functions and the size of the ordinals for which they can provide representations.

The purpose of this paper is to show that, for any integer n, the ordinal (see §2) is a bound for the closure ordinals of replete monotonic increasing n-place functions. This result is optimal for n > 2 (the bound is attained by where θα = 1 + α) but not for n < 2. D. H. de Jongh has recently proved, using a completely different method, that the (least possible) bound for n = 2 is ε0. (Trivially, that for n = 1 is φ.)

In [4] it is shown that if the structure omits a type Σ, and Σ is complete with respect to Th(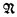), then there is a proper elementary extension of which omits Σ. This result is extended in the present paper. It is shown that Th() has models omitting Σ in all infinite powers.

A type is a countable set of formulas with just the variable ν occurring free. A structure is said to omit the type Σ if no element of satisfies all of the formulas of Σ. A type Σ, in the same language as a theory T, is said to be complete with respect to T if (1) T ∪ Σ is consistent, and (2) for every formula φ(ν) of the language of T (with just ν free), either φ or ¬φ is in Σ.

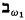The proof of the result of this paper resembles Morley's proof [5] that the Hanf number for omitting types is . It is shown that there is a model of Th() which omits Σ and contains an infinite set of indiscernibles. Where Morley used the Erdös-Rado generalization of Ramsey's theorem, a definable version of the ordinary Ramsey's theorem is used here.

The “omitting types” version of the ω-completeness theorem ([1], [3], [6]) is used, as it was in Morley's proof and in [4]. In [4], satisfaction of the hypotheses of the ω-completeness theorem followed from the fact that, in , any infinite, definable set can be split into two infinite, definable sets.

The primary purpose of this work is to analyze the constructive interpretations of classical theorems concerning the continuity of effective operations. These theorems are the “recursivizations” of the statements that all functions (on various spaces) are continuous. To discuss the question whether these statements are constructively valid, it would be necessary to analyze the notion of “constructively valid,” which is beyond the scope of this paper. We now proceed to describe our results. We deal with two kinds of effective operations: (i) partial operations on indices of partial functions, and (ii) total operations on indices of total functions. The two principal theorems of the subject assert that each such operation is continuous; for (i) this is due to Myhill-Shepherdson [7] and called MS here; for (ii) it is due to Kreisel, Lacombe, and Shoenfield [5] and called KLS. (Explicit formulations of these and other principles mentioned in the introduction will be given in §1 below.)

Several interpretations (of, e.g., Heyting's arithmetic HA) in the literature satisfy Markov's principle MP, and for these MS and KLS are valid, since a close inspection of the classical proofs of MS and KLS shows that they are derivable in HA + MP. But we also find an interpretation in the literature under which MS and KLS are valid while MP is not (hence MS and KLS do not imply MP in systems for which this interpretation is sound). This work is in §2.

This paper is the third in a series collectively entitled Formal systems of intuitionistic analysis. The first two are [4] and [5] in the bibliography; in them I attempted to codify Brouwer's mathematical practice. In the present paper, which is independent of [4] and [5], I shall do the same for Bishop's book [1]. There is a widespread current impression, due partly to Bishop himself (see [2]) and partly to Goodman and the author (see [3]) that the theory of Gödel functionals, with quantifiers and choice, is the appropriate formalism for [1]. That this is not so is seen as soon as one really tries to formalize the mathematics of [1] in detail. Even so simple a matter as the definition of the partial function 1/x on the nonzero reals is quite a headache, unless one is prepared either to distinguish nonzero reals from reals (a nonzero real being a pair consisting of a real x and an integer n with ∣x∣ > 1/n) or, to take the Dialectica interpretation seriously, by adjoining to the Gödel system an axiom saying that every formula is equivalent to its Dialectica interpretation. (See [1, p. 19], [2, pp. 57–60] respectively for these two methods.) In more advanced mathematics the complexities become intolerable.

In [3] we have associated to a structure an ordinal which gives us information about elementary substructures of the structure. For example a structure whose ascending chain number (as we call the ordinal) is ω could be called Noetherian since all ascending elementary chains inside it are finite (and there are arbitrarily large finite chains). Theorem 2 shows that such structures exist. In fact we prove that for any α < ω1 there is a structure whose ascending chain number is α. The construction is based on the existence of a certain group of permutations of ω (see Theorem 1). The second part of this paper deals with the relevance of the chain number to the study of Jonsson algebras.

Here we prove the following:

Theorem. For every N ≤ ω there is a complete theory Tn having exactly n nonisomorphic rigid models and no uncountable rigid models. Moreover, each non-rigid model admits a nontrivial automorphism.

The Tn are theories in the first-order predicate calculus and a rigid structure is a structure with no nontrivial endomorphisms, i.e., the only endomorphism of the structure into itself is the identity. The theorem answers a question of A. Ehrenfeucht.

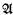For the most part we use standard model theoretic notation with Th denoting the set of sentences true in and meaning . A complete set of sentences is one of the form Th for some . The universe of a structure may be denoted by ∣∣. An n-ary relation on X is a set of n tuples (x0, …, xn−1) with each xi ∈ X. All the structures encounted here will be relational. If P is an n-ary relation then P ↾ Y, the restriction of P to Y, is {(x0, …, xn−1): (x0, …, xn−1) ∈ P and x0, …, xn−1Y}.

The aim of this paper is to correct an error in the proof in [2] of a strengthened version of Hilbert's second ε-theorem.

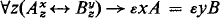Hilbert's original theorem says (effectively) that formulae of the form ∃xA → A(εxA) can be eliminated from deductions of ∈-free sentences B (i.e. those which do not contain the ε-symbol) from collections X of ε-free sentences. The extended version (Theorem III. 11 of [2]) says that, in addition, instances of Ackermann's schema can also be eliminated.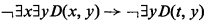

The error in [2] occurs in the proof of Theorem III.7 and is described as follows. If A′ is the formula obtained from A by replacing every occurrence of ∃yB by B(εyB) (or ∀yC by C(εyB) if B is of the form ¬ C), and if A is a Q3 or Q4-axiom then, contrary to the claim on p. 73 of [2], A′ is not necessarily an axiom of the same form. For example, if A is the Q3-axiom

where the rank of εx∃yD(x, y) is ≤ the rank of εyB (see p. 70) and where B is D(t,y), then A′ is

which is not a Q3-axiom. In other words, the notion of rank as defined in [2] is inadequate for the proof of Theorem III.11.

This note is concerned with an aspect of the length of proof of formulas in recursively enumerable theories T adequate for recursive arithmetic. In particular, we consider the relative length of proof of formulas in the theories T and T(S), where F represents an r.e. set A in T and T(S) is the theory obtained from T by adjunction, as a new axiom, of a sentence S undecidable in T.

Throughout the sequel T is a consistent, r.e. theory with standard formalization [7] in which all recursive functions of one variable are definable, and in which there is a binary formula x ≤ satisfying the well-known conditions [7]:

Here is the constant term corresponding to the natural number n. Wn is the nth r.e. set in a standard enumeration of the r.e. sets. Also, we assume an a priori Gödel numbering of our formalism satisfying the usual conditions, so that all formulas are numbers ab initio.

In the more common applications of the theorem below, if F is a k-ary formula of T, is a natural number that measures in some way the length of the shortest proof of in T.

Sacks [2] has asked whether there exists a uniform solution to Post's problem, i.e. an enumeration operation W such that d < W(d) < d′ for every degree d. It is shown here that if such an operation W exists it cannot itself in a particular technical sense be uniform. In fact, the jump operation is characterized amongst such uniform enumeration operations by the condition: d < W(d) for all d. In addition, it is proved that the only other uniform enumeration operations such that d ≤ W(d) for all d are those which equal the identity operation above some fixed degree.

Much effort has been spent to prove that the reduced product operation preserves, and sometimes even strengthens the L-equivalence of structures, where L is some infinitary language. A similar result is suggested by the following well-known fact:

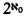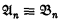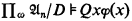Assume D is a nonprincipal ultrafilter on ω and, for n Є ω, Cn is a set. If the ultra-product ΠωCn/D is infinite, it has a cardinality ≥ Hence, by Łos' theorem, (i) if and φ(x) is a first-order formula, then iff 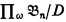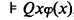where Q is the unary quantifier “there are many.”

We shall prove some generalizations of (i). In particular, we show

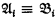(ii) if D is a nonprincipal ultrafilter over I = ω, and then 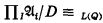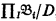where L(Q) is the language obtained from the first-order language by adding the quantifier Q.

(ii) remains true, if D is an ω-regular or an atomless filter over a set I.

Lipner [7] proved that if is regular, then the L(Q)-equivalence is preserved under direct products. We show that the assumption “ is regular” is necessary.

The study of countable theories categorical in some uncountable power was initiated by Łoś and Vaught and developed in two stages. First, Morley proved (1962) that a countable theory categorical in some uncountable power is categorical in every uncountable power, a conjecture of Łoś. Second, Baldwin and Lachlan confirmed (1969) Vaught's conjecture that a countable theory categorical in some uncountable power has either one or countably many isomorphism types of countable models. That result was obtained by pursuing a line of research developed by Marsh (1966). For certain well-behaved theories, which he called strongly minimal, Marsh's method yielded a simple proof of Łoś's conjecture and settled Vaught's conjecture.

In recent years efforts have been made to extend these results to uncountable theories. The generalized Łoś conjecture states that a theory T categorical in some power greater than ∣T∣ is categorical in every such power. It was settled by Shelah (1970). Shelah then raised the question of the models in power ∣T∣ = ℵα of a theory T categorical in ∣T∣+, conjecturing in [S3] that there are exactly ∣α∣ + ℵ0 such models, up to isomorphism. This conjecture provided the initial motivation for the present work. We define and study semi-minimal theories analogous in some ways to Marsh's strongly minimal (countable) theories. We describe the models of a semi-minimal theory T which contain an infinite indiscernible set. Besides throwing some light on Shelah's conjecture, our method gives simple proofs of the Łoś conjecture and of the Morley conjecture on categoricity in ∣T∣, in the case of a semi-minimal theory T. Other results as well as some examples are provided.

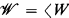§1. A complete atomic modal algebra (CAMA) is a complete atomic Boolean algebra with an additional completely additive unary operator. A (Kripke) frame is just a binary relation on a nonempty set. If is a frame, then 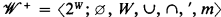is a CAMA, where 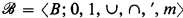mX = {y ∣ (∃x)(y < x Є X)}; and if is a CAMA then 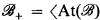is a frame, where 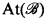is the set of atoms of 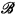and b1 < b2 ⇔ b1 ∩ mb2 ≠∅.

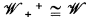Now , and 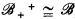the validity of a modal formula on 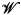is equivalent to the satisfaction of a modal algebra polynomial identity by 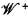and conversely, so the validity-preserving constructions on frames ought to be in some sense equivalent to the identity-preserving constructions on CAMA's. The former are important for modal logic, and many of the results of universal algebra apply to the latter, so it is worthwhile to fix precisely the sense of the equivalence.

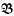The most important identity-preserving constructions on CAMA's can be described in terms of homomorphisms and complete homomorphisms. Let and 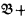be the categories of CAMA's with homomorphisms and complete homomorphisms, respectively. We shall define categories and of frames with appropriate morphisms, and show them to be dual respectively to and . Then we shall consider certain identity-preserving constructions on CAMA's and attempt to describe the corresponding validity-preserving constructions on frames.

The proofs of duality involve some rather detailed calculations, which have been omitted. All the category theory a reader needs to know is in the first twenty pages of [7].

Although a variety of proofs are available for the Craig-Lyndon Interpolation Lemma, they all seem to make essential use of negation, with the result that they are inapplicable to deductive theories in which negation cannot be expressed. It is here shown that this use of negation can be avoided by extending the Interpolation Lemma to the pure implicational calculus PCI.

Determinate Parameter Lemma. For each formula A, ⊨PA ⊃ A for some sentence parameter PA occurring in A.

Proof. By induction on the construction of A.

Interpolation Lemma For PCI. Let Γ be the set of sentence parameters common to A and C.If ⊨A ⊃ and C is not valid, then there is a formula B containing no sentence parameter not in Y such that ⊨A ⊃ B and ⊨B ⊃ C.

Proof. Since ⊨PA ⊃ A by the Determinate Parameter Lemma and ⊨A ⊃ C, ⊨PA ⊃ C. But C is by hypothesis an invalid formula, so PA must occur in C as well as in A. Thus PA Є Γ.