No CrossRef data available.
Article contents
L(Q)-preservation theorems
Published online by Cambridge University Press: 12 March 2014
Extract
Much effort has been spent to prove that the reduced product operation preserves, and sometimes even strengthens the L-equivalence of structures, where L is some infinitary language. A similar result is suggested by the following well-known fact:
Assume D is a nonprincipal ultrafilter on ω and, for n Є ω, Cn is a set. If the ultra-product ΠωCn/D is infinite, it has a cardinality ≥ 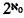 Hence, by Łos' theorem, (i) if
Hence, by Łos' theorem, (i) if 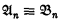 and φ(x) is a first-order formula, then
and φ(x) is a first-order formula, then 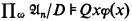 iff
iff 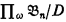
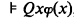 where Q is the unary quantifier “there are
where Q is the unary quantifier “there are 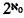 many.”
many.”
We shall prove some generalizations of (i). In particular, we show
(ii) if D is a nonprincipal ultrafilter over I = ω, and 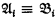 then
then 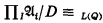
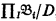 where L(Q) is the language obtained from the first-order language by adding the quantifier Q.
where L(Q) is the language obtained from the first-order language by adding the quantifier Q.
(ii) remains true, if D is an ω-regular or an atomless filter over a set I.
Lipner [7] proved that if 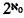 is regular, then the L(Q)-equivalence is preserved under direct products. We show that the assumption “
is regular, then the L(Q)-equivalence is preserved under direct products. We show that the assumption “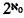 is regular” is necessary.
is regular” is necessary.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1975


