Research Article
Definability in low simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1481-1490
-
- Article
- Export citation
A polarized partition relation using elementary substructures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1491-1498
-
- Article
- Export citation
Admissibility of structural rules for contraction-free systems of intuitionistic logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1499-1518
-
- Article
- Export citation
Inconsistent models of arithmetic Part II: the general case
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1519-1529
-
- Article
- Export citation
Topological elementary equivalence of closed semi-algebraic sets in the real plane
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1530-1555
-
- Article
- Export citation
Logics of belief change without linearity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1556-1575
-
- Article
- Export citation
All intermediate logics with extra axioms in one variable, except eight, are not strongly ω-complete
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1576-1604
-
- Article
- Export citation
Computable Boolean algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1605-1623
-
- Article
- Export citation
Applications of PCF theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1624-1674
-
- Article
- Export citation
Le problème des grandes puissances et celui des grandes racines
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1675-1685
-
- Article
- Export citation
Strong 0-1 laws in finite model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1686-1704
-
- Article
- Export citation
A note on equational theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1705-1712
-
- Article
- Export citation
More on Cichoń's diagram and infinite games
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1713-1724
-
- Article
- Export citation
On the commutativity of jumps
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1725-1748
-
- Article
- Export citation
Epsilon-logic is more expressive than first-order logic over finite structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1749-1757
-
- Article
- Export citation
A model complete theory of valued D-fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1758-1784
-
- Article
- Export citation
Interpreting classical theories in constructive ones
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1785-1812
-
- Article
- Export citation
◇ at Mahlo cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1813-1822
-
- Article
- Export citation
More on entangled orders
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1823-1832
-
- Article
- Export citation
Minimal fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1833-1835
-
- Article
- Export citation

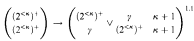
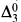 Boolean algebra need not have a computable copy (see also [T
Boolean algebra need not have a computable copy (see also [T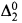 with certain added predicates can be embedded in one which is
with certain added predicates can be embedded in one which is 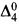 , at worst, and the same is true for a low
, at worst, and the same is true for a low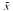 = (
= (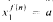 de
de 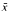 . Ce sont deux exemples de problèmes que l'utilisation de la dérivée ne permet pas de résoudre plus rapidement. Nous montrons que le problème des grandes racines n'est pas polynomial au sens des corps differentiels, même si nous autorisons un nombre polynomial de paramètres. et que le problème des grandes puissances n'est pas polynomial au sens des corps differentiels. même au niveau non uniforme. Les démonstrations utilisent la stabilité polynomial de la théorie des corps de caractéristique nulle. montrée par L. Blum, F. dicker. M. Shub et S. Smale, ainsi que le lemme de réduction qui permet de ramener un polynôme differentiel des variables
. Ce sont deux exemples de problèmes que l'utilisation de la dérivée ne permet pas de résoudre plus rapidement. Nous montrons que le problème des grandes racines n'est pas polynomial au sens des corps differentiels, même si nous autorisons un nombre polynomial de paramètres. et que le problème des grandes puissances n'est pas polynomial au sens des corps differentiels. même au niveau non uniforme. Les démonstrations utilisent la stabilité polynomial de la théorie des corps de caractéristique nulle. montrée par L. Blum, F. dicker. M. Shub et S. Smale, ainsi que le lemme de réduction qui permet de ramener un polynôme differentiel des variables 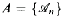 } of finite models, where the universe of
} of finite models, where the universe of 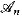 is {1,2, …, n}. and use this framework to strengthen 0-1 laws for logics.
is {1,2, …, n}. and use this framework to strengthen 0-1 laws for logics.