Research Article
Relational semantics and a relational proof system for full Lambek calculus
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 623-637
-
- Article
- Export citation
Ultrafilters which extend measures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 638-662
-
- Article
- Export citation
An absoluteness principle for Borel sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 663-693
-
- Article
- Export citation
A many permutation group result for unstable theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 694-708
-
- Article
- Export citation
Frege proof system and TNC°
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 709-738
-
- Article
- Export citation
A note on valuation definable expansions of fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 739-743
-
- Article
- Export citation
Reviews
Ehud Hrushovski, The Mordell–Lang conjecture for function fields. Journal of the American Mathematical Society, vol. 9 (1996), pp. 667–690.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 744-746
-
- Article
- Export citation
David Marker, Introduction to the model theory of fields. Model theory of fields, Lecture notes in logic, no. 5, Springer, Berlin, Heidelberg, New York, etc., 1996, pp. 1–37. - David Marker. Model theory of differential fields. Model theory of fields, Lecture notes in logic, no. 5, Springer, Berlin, Heidelberg, New York, etc., 1996, pp. 38–113. - Anand Pillay. Differential algebraic groups and the number of countable differentially closed fields. Model theory of fields, Lecture notes in logic, no. 5, Springer, Berlin, Heidelberg, New York, etc., 1996, pp. 114–134. - Margit Messmer. Some model theory of separably closed fields. Model theory of fields, Lecture notes in logic, no. 5, Springer, Berlin, Heidelberg, New York, etc., 1996, pp. 135–152.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 746-747
-
- Article
- Export citation
Yuri L. Ershov. Definability and computability. English translation of Opredelimost′ i vychislimost′. Siberian school of algebra and logic. Consultants Bureau, New York, London, and Moscow, 1996, xiv + 264 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 747-748
-
- Article
- Export citation
Yuriĭ L. Ershov. Opredelimost′ i rychislimost′. Russian original of the preceding. Sibirskaya shkola algebry i logiki. Nauchnaya Kniga, Novosibirsk 1996, 300 pp. - Richard Lassaigne and Michel de Rougemont. Logique et complexité. Collection informatique. Hermès, Paris 1996, viii + 322 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 748
-
- Article
- Export citation
L. A. Harrington, A. S. Kechris, and A. Louveau. A Glimm–Effros dichotomy for Borel equivalence relations. Journal of the American Mathematical Society, vol. 3 (1990), pp. 903–928. - Alain Louveau and Boban Velickovic. A note on Borel equivalence relations. Proceedings of the American Mathematical Society, vol. 120 (1994), pp. 255–259. - Alexander S. Kechris and Alain Louveau. The classification ofhypersmooth equivalence relations. Journal of the American Mathematical Society, vol. 10 (1997), pp. 215–242.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 749-750
-
- Article
- Export citation
S. Todorchevich and I. Farah. Some applications of the method of forcing. Series in pure and applied mathematics. Yensei, Moscow 1995, also distributed by Bid International Co., Sherman Oaks, Calif., viii + iii + 148 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 750-751
-
- Article
- Export citation
Luis E. Sanchis. Set theory—an operational approach. Gordon and Breach Science Publishers, Amsterdam etc. 1996, xvi + 279 pp.
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 751-752
-
- Article
- Export citation
Front matter
JSL volume 63 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
JSL volume 63 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation

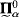 set can be introduced into the
set can be introduced into the 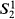 and showed that
and showed that 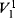 (
(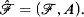 .
.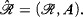 .
.