Article contents
Weak strong partition cardinals
Published online by Cambridge University Press: 12 March 2014
Extract
In a series of papers [K2], [K3], [K4], E. M. Kleinberg established the extensive properties of what are now called “strong partition cardinals”, cardinals satisfying 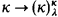 for all λ < κ. The purpose of this note is to show that all these consequences and the results in [H] and [W] can be obtained from the weaker relation
for all λ < κ. The purpose of this note is to show that all these consequences and the results in [H] and [W] can be obtained from the weaker relation 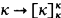 and many from
and many from 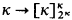 .
.
We assume the reader is generally familiar with Kleinberg's machinery and with the definition of 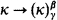 . We recall that a cardinal κ satisfies
. We recall that a cardinal κ satisfies 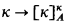 iff for every partition F: [κ]κ → A there is a p ∈ [κ]κ such that F″ [p]κ ≠ A. We take the liberty of regarding a p ∈ [κ]κ both as a subset of κ and as a function from κ to κ. We assume DC throughout.
iff for every partition F: [κ]κ → A there is a p ∈ [κ]κ such that F″ [p]κ ≠ A. We take the liberty of regarding a p ∈ [κ]κ both as a subset of κ and as a function from κ to κ. We assume DC throughout.
§1. From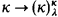 . Our results stem from the observation that the proofs in the papers cited above only require homogeneous sets for certain classes of partitions.
. Our results stem from the observation that the proofs in the papers cited above only require homogeneous sets for certain classes of partitions.
Definition. A partition F: [κ]κ → λ, λ < λ, is called clopen if for all p ∈ [κ]κ there is an α < κ such that whenever 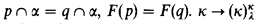 -clopen is the assertion that all clopen partitions have homogeneous sets (Spector-Watro).
-clopen is the assertion that all clopen partitions have homogeneous sets (Spector-Watro).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984
References
REFERENCES
- 1
- Cited by


