Article contents
Variations on a theme by Weiermann
Published online by Cambridge University Press: 12 March 2014
Abstract
Weiermann [18] introduces a new method to generate fast growing functions in order to get an elegant and perspicuous proof of a bounding theorem for provably total recursive functions in a formal theory, e.g., in PA. His fast growing function θαη is described as follows. For each ordinal a and natural number n let 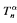 denote a finitely branching, primitive recursive tree of ordinals, i.e., an ordinal as a label is attached to each node in the tree so that the labelling is compatible with the tree ordering. Then the tree
denote a finitely branching, primitive recursive tree of ordinals, i.e., an ordinal as a label is attached to each node in the tree so that the labelling is compatible with the tree ordering. Then the tree 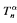 is well founded and hence finite by König's lemma. Define θαηn =the depth of the tree
is well founded and hence finite by König's lemma. Define θαηn =the depth of the tree 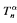 =the length of the longest branch in
=the length of the longest branch in 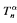 .
.
We introduce new fast and slow growing functions in this mode of definitions and show that each of these majorizes provably total recursive functions in PA.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
- 3
- Cited by


