Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-20T16:29:45.402Z Has data issue: false hasContentIssue false
  • English
  • Français

The Motivic Cohomology of Stiefel Varieties

Published online by Cambridge University Press:  21 November 2011

Ben Williams
Ben Williams*
Affiliation:
USC, Department of Mathematics, Kaprielian Hall, 3620 South Vermont Avenue, Los Angeles, CA [email protected]
Get access

Abstract

The main result of this paper is a computation of the motivic cohomology of varieties of n × m-matrices of of rank m, including both the ring structure and the action of the reduced power operations. The argument proceeds by a comparison of the general linear group-scheme with a Tate suspension of a space which is 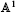-equivalent to projective n — 1-space with a disjoint basepoint.

Keywords

Motivic cohomologyhigher Chow groupsreduced power operationsStiefel varieties
Type
Research Article
Information
Journal of K-Theory , Volume 10 , Issue 1 , August 2012 , pp. 141 - 163
Copyright
Copyright © ISOPP 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ada62.Adams, J. F., Vector fields on spheres, Ann. of Math. 75 (1962), 603–632.CrossRefGoogle Scholar
Blo86.Bloch, S., Algebraic cycles and higher K-theory, Advances in Mathematics 61 (1986), 267–304.CrossRefGoogle Scholar
Blo94.Bloch, S., The moving lemma for higher Chow groups, Journal of Algebraic Geometry 3 (1994), 537–568.Google Scholar
Del.Deligne, P., Lectures on motivic cohomology 2000/2001, www.math.uiuc.edu/K-theory/0527.Google Scholar
DHI04.Dugger, D., Hollander, S. and Isaksen, D. C., Hypercovers and simplicial presheaves, Math. Proc. Cambridge Philos. Soc. 136 (2004), 9–51.Google Scholar
Ful84.Fulton, W., Intersection Theory, Springer Verlag (1984).Google Scholar
Gro61.Grothendieck, A., Éléments de géométrie algébrique. II. Étude globale élémentaire de quelques classes de morphismes, Inst. Hautes Études Sci. Publ. Math. 222 (1961).Google Scholar
Har77.Hartshorne, R., Algebraic Geometry, Gradute Texts in Mathematics 52, Springer Verlag (1977).Google Scholar
Jam76.James, I. M., The Topology of Stiefel Manifolds, Cambridge University Press, Cambridge, England (1976).Google Scholar
MV99.Morel, F. and Voevodsky, V., -homotopy theory of schemes, Inst. Hautes Études Sci. Publ. Math. 90 (2001), 45–143.Google Scholar
MVW06.Mazza, C., Voevodsky, V. and Weibel, C., Lectures on Motivic Cohomology, Clay Monographs in Math. 2, AMS (2006).Google Scholar
Pus04.Pushin, O., Higher Chern classes and Steenrod operations in motivic cohomology, K-Theory 31 (2004), 307–321.Google Scholar
Ray68.Raynaud, M., Modules projectifs universels, Invent. Math. 6 (1968), 1–26.Google Scholar
Voe02.Voevodsky, V., Motivic cohomology are isomorphic to higher Chow groups in any characteristic, International Mathematics Research Notices 7 (2002), 351–355.Google Scholar
Voe03.Voevodsky, V., Reduced power operations in motivic cohomology, Publications Mathématiques de l’IHÉS 98 (2003), 1–57.Google Scholar
Wei99.Weibel, C. A., Products in higher Chow groups and motivic cohomology, in: Algebraic K-theory, Seattle WA 1997, Proceedings of Symposia in Pure Mathematics, American Mathematical Society (1999), 305–315.Google Scholar