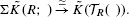Let A be a ring with anti-involution and F a nice functor (tensor or symmetric power, for example) from finitely-generated projective A-modules to abelian groups. We show that the homology of the hyperbolic unitary groups Un,n(A) with coefficients in F(A2n) can be expressed stably (i.e. after taking the colimit over n) by the homology of these groups with untwisted coefficients and functor homology groups that we can compute in suitable cases (for example, when A is a field of characteristic 0 or a ring without ℤ-torsion and F a tensor power). This extends the result where A is a finite field, which was dealt with previously by C. Vespa and the author (Ann. Sci. ENS, 2010).
The proof begins by relating, without any assumption on F, our homology groups to the homology of a category of hermitian spaces with coefficients twisted by F. Then, when F is polynomial, we establish — following a method due to Scorichenko — an isomorphism between this homology and the homology of another category of (possibly degenerate) hermitian spaces, which is computable (in good cases) by standard methods of homological algebra in functor categories (using adjunctions, Künneth formula…). We give some examples.
Finally, we deal with the analogous problem for non-hyperbolic unitary groups in some special cases, for example euclidean orthogonal groups On (A) (the ring A being here commutative). The isomorphism between functor homology and group homology with twisted coefficients does not hold in full generality; nevertheless we succeed to get it when A is a field or, for example, a subring of ℚ containing ℤ[1/2]. The method, which is similar to that in the previous case, uses a general result of symmetrisation in functor homology proved at the beginning of the article.


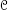 ,⊗, 1) One of the key ingredients of this theory is the definition of a Zariski topology on the category of commutative monoidal objects in
,⊗, 1) One of the key ingredients of this theory is the definition of a Zariski topology on the category of commutative monoidal objects in 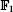 in [D] and in [TV].
in [D] and in [TV].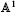 -equivalent to projective
-equivalent to projective 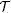
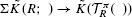 which is closely related to Waldhausen's equivalence
which is closely related to Waldhausen's equivalence 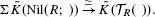 We show that Φ induces an equivalence on any finite stage of Goodwillie's Taylor towers of the functors at any simplicial bimodule. This is used to show that there is an equivalence of functors
We show that Φ induces an equivalence on any finite stage of Goodwillie's Taylor towers of the functors at any simplicial bimodule. This is used to show that there is an equivalence of functors 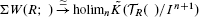 , and for connected bimodules, also an equivalence
, and for connected bimodules, also an equivalence